

书名:计算流体力学大串讲
ISBN:978-7-115-66704-5
本书由人民邮电出版社发行数字版。版权所有,侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用,未经授权,不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟,与我们共同保护知识产权。
如果购买者有侵权行为,我们可能对该用户实施包括但不限于关闭该帐号等维权措施,并可能追究法律责任。
著 田 东
责任编辑 胡俊英
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
网址 http://www.ptpress.com.cn
读者服务热线:(010)81055410
反盗版热线:(010)81055315
计算流体力学(Computational Fluid Dynamics,CFD)是一门交叉学科,融合了流体力学、数值分析与计算机技术,致力于通过数学建模和数值模拟解决复杂流体流动问题。它不仅推动了航空航天、机械工程、能源开发等领域的技术进步,也为现代科学研究提供了强有力的支持。本书以深入浅出的方式,系统阐述了计算流体力学的基本理论与核心方法,旨在为读者开启一扇通往流体模拟世界的大门。
全书共分8章,内容层层递进。第1章从动力学基础出发,引入流体力学的基本概念。第2章深入探讨连续性方程、动量方程与能量守恒方程等偏微分方程的推导与特性。第3章聚焦计算区域与控制方程的离散化方法。第4、5章分别介绍有限差分法、有限体积法及代数方程组的求解技术。第6~8章则围绕扩散问题、对流-扩散问题及压力-速度耦合问题展开详细讨论。
本书适合高校相关专业的本科生与研究生作为参考教材使用,也可供科研人员和工程技术人员参阅。无论是初学者还是有一定基础的读者,都能从本书中获得有用的理论知识和可借鉴的实践方法。
这是一本非传统的计算流体力学图书,笔者在编写本书的时候,力求详细再详细,力求让读者能够自学本书,并在学习过程中找到自信。这本书能够顺利面世,我要感谢很多人。
感谢北京航空航天大学何允钦老师的鼓励,何老师帮我总览了全稿,提出了很多宝贵的意见,令晚辈心生敬意。
感谢同济大学的操金鑫老师,操老师治学严谨,他对书稿提出了很多细节性的修改意见。
感谢上海交通大学的王景老师,王老师教我如何使用MATLAB,告诉我有限体积法的总体思想,王老师对代码、CFD原理都有独到的见解。每次我遇到科研问题,王老师都能够快速定位我的核心问题,并帮我答疑解惑。在本书的审校过程中,对于书中的错别字、错误的公式和字母表达,王老师都一一帮我标记了出来。
感谢美国锡拉丘兹大学(又称“雪城大学”)的林童师兄,他教会我Fluent的基本原理和使用方法,在我求解遇到问题的时候,他总是非常耐心地给我解答,并能够快速解决困扰我很久的问题。
感谢人民邮电出版社的工作人员,他们对书稿提出了很多修改意见,使得书稿更符合出版要求。
由于我本人能力所限,书中的内容难免存在考虑不够周全、处理有欠妥当的地方,诚恳地希望得到广大读者的批评与指正,欢迎大家在B站(昵称“田东Joshua”)与我交流,以帮助本书不断迭代、优化。
希望这本书可以作为你入门CFD知识的第一本书,帮你打开CFD的斑斓世界。
田东
本书提供如下资源:
● 案例素材;
● 配套彩图;
● 本书思维导图;
● 异步社区7天VIP会员。
要获得以上资源,您可以扫描下方二维码,根据指引领取。

作者和编辑尽最大努力来确保书中内容的准确性,但难免会存在疏漏。欢迎您将发现的问题反馈给我们,帮助我们提升图书的质量。
当您发现错误时,请登录异步社区(https://www.epubit.com),按书名搜索,进入本书页面,单击“发表勘误”,输入错误信息,单击“提交勘误”按钮即可(见下图)。本书的作者和编辑会对您提交的错误信息进行审核,确认并接受后,您将获赠异步社区的100积分。积分可用于在异步社区兑换优惠券、样书或奖品。
我们的联系邮箱是contact@epubit.com.cn。
如果您对本书有任何疑问或建议,请您发邮件给我们,并请在邮件标题中注明本书书名,以便我们更高效地做出反馈。
如果您有兴趣出版图书、录制教学视频,或者参与图书翻译、技术审校等工作,可以发邮件给我们。
如果您所在的学校、培训机构或企业,想批量购买本书或异步社区出版的其他图书,也可以发邮件给我们。
如果您在网上发现有针对异步社区出品图书的各种形式的盗版行为,包括对图书全部或部分内容的非授权传播,请您将怀疑有侵权行为的链接发邮件给我们。您的这一举动是对作者权益的保护,也是我们持续为您提供有价值的内容的动力之源。
“异步社区”是由人民邮电出版社创办的IT专业图书社区,于2015年8月上线运营,致力于优质内容的出版和分享,为读者提供高品质的学习内容,为作译者提供专业的出版服务,实现作者与读者在线交流互动,以及传统出版与数字出版的融合发展。
“异步图书”是异步社区策划出版的精品IT图书的品牌,依托于人民邮电出版社在计算机图书领域的发展与积淀。异步图书面向IT行业以及各行业使用IT的用户。
大概三年前,我想找到一句描述计算流体力学(Computational Fluid Dynamics,CFD)让人痴迷、让人甘愿花费时间沉浸其中的句子。直到有一天,我走在路上,想起秦观《鹊桥仙·纤云弄巧》中的“金风玉露一相逢,便胜却人间无数”,这句词既含有空气又含有水,包含了CFD主要的研究对象。我大喜过望,身心都愉悦起来!当然,这首词还有更为大众所熟知的语句——两情若是久长时,又岂在朝朝暮暮。
我们每天的行为会受意识支配,比如上小学时,早上我们从家去学校,当面对走哪条路更近的问题时,意识会帮助我们判断并做出决定[见图1-1(A)]。中学时代学习牛顿第二定律时,当质量为m的小滑块受到力F的作用时,我们就可以算出它的加速度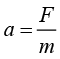 [图1-1(B)]。
[图1-1(B)]。
意识控制着人的行为,力控制着固体的运动,那么什么控制着流体的运动呢?我们呼吸的空气,河里流动的水,这些都是流体,那是什么在支配着它们的运动呢[见图1-1(C)]?
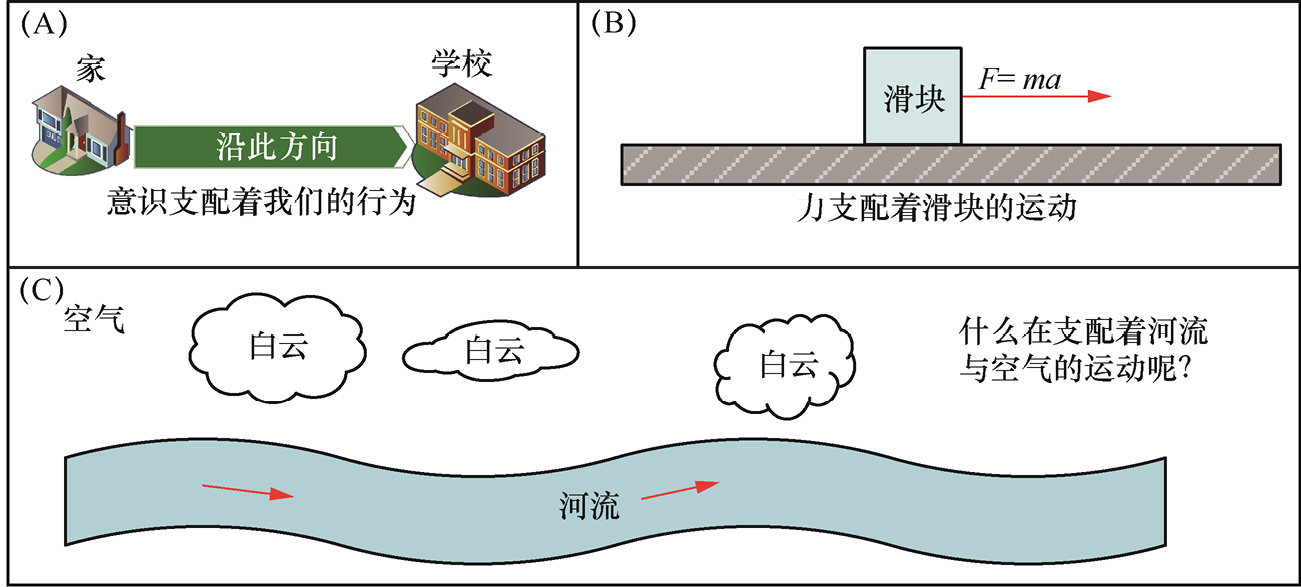
图1-1 意识控制着人的行为,方程控制着物质的运动
答案是三大方程支配着流体的运动,它们分别是:
● 连续性方程(质量守恒方程);
● 动量守恒方程(Navier-Stokes方程,简称N-S方程);
● 能量守恒方程。
原则上,我们只需要求解支配流体运动的三大方程,就可以洞见流体的一举一动,预测它们的运动,甚至控制它们,真正做到“御风而行”。而我们将要学习的CFD就是专门研究流体运动的学问。
CFD主要是借助计算机来求解上面所说的三大方程。接下来我们将花费大量的工夫来推导这些方程。霍金曾认为,书里每多一个数学公式,这本书的销量就会减半。杨振宁先生也曾提到类似的观点——有两类数学著作,一类是你看完第一页就不想看下去了,另一类是你看完第一句话就不想看下去了。我们学习CFD,要接触大量的公式,这让很多数学基础不好的同学犯了难。不过你不要担心,不要害怕。笔者力求把书写得详细,争取让大家都能够看懂,相信你在阅读本书后面的内容时,会慢慢感受到这一点。在正式推导三大方程之前,我们需要掌握一些辅助知识。下面先来看看质量流量和体积流量的概念。
我们先回忆小学就接触过的质量概念:
质量=密度×体积
用符号表示就是
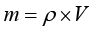 (1-1)
(1-1)
在式(1-1)中,m为质量,单位为kg;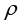 为密度,单位为kg/m3;V为体积,单位为m3。
为密度,单位为kg/m3;V为体积,单位为m3。
当我们研究流体时,更关注流体运动的过程,就要在质量概念的基础上再往前推进一步。我们用质量流量来描述流体单位时间流进/流出某截面的质量。如图1-2所示,早上我们打开水龙头洗漱,水龙头出水口的横截面积记为A,单位为m2;出水口流体的速度记为U,单位为m/s;水的密度记为ρ,单位为kg/m3。为了方便计算,我们取A=0.001m2,U=3m/s,ρ=1000kg/m3。如果水龙头打开的时间段Δt等于2s,那么在这2s内,我们一共接了多少水呢?也就是水池中积了多少千克的水呢?这个问题用初中物理知识就可以解决。

图1-2 水龙头出水
根据前面的介绍,水的质量计算公式可以表示成
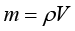
从上式可以看出,在密度ρ已知的情况下,要想求质量m,关键是求出在时间段Δt=2s内从水龙头流出的水的体积V。水从水龙头出来形成一个水柱(假设水流不被打断,且假设水流截面积保持不变),我们知道对于柱体而言,体积等于底面积乘以高。底面积就是水龙头的出水的横截面积A,高应该为多少呢?水的速度为U,时间段为Δt,那么在Δt内,水流过的距离就是高,应该等于UΔt。于是可得水柱的体积为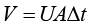 。进而可得水的质量为
。进而可得水的质量为
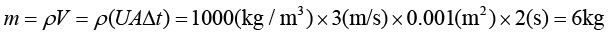
如果水龙头打开的时间段Δt等于5s,那么在这5s内,一共接了多少水呢?我相信聪明的你一定会计算,只需要把Δt换成5s代入就行,即
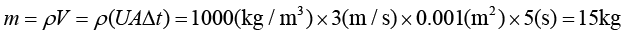
通过比较,我们发现,如果水龙头开启的时间段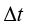 不同,流到水池中的水的质量就不同,也就是水的质量会随着时间而改变。那么单位时间内从水龙头出来的流量该怎么求呢?这就引出了质量流量的概念。只需要把方程
不同,流到水池中的水的质量就不同,也就是水的质量会随着时间而改变。那么单位时间内从水龙头出来的流量该怎么求呢?这就引出了质量流量的概念。只需要把方程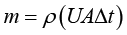 等号右边的
等号右边的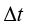 除到等号左边就行了,即
除到等号左边就行了,即
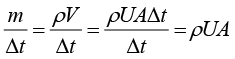
我们引入一个新的符号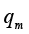 表示质量流量,有
表示质量流量,有
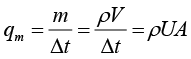
对于上式,只取首尾,可得
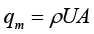 (1-2)
(1-2)
式(1-2)就是质量流量的表达式。
因为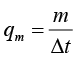 ,其中分子m的单位为kg,分母Δt的单位为s,所以质量流量
,其中分子m的单位为kg,分母Δt的单位为s,所以质量流量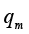 的单位为kg/s。我们可以进一步延伸推导出体积流量的表达式。由于质量和体积之间相差一个密度,类比可知质量流量和体积流量之间也相差一个密度,所以只需用质量流量除以流体密度,就可以得到体积流量
的单位为kg/s。我们可以进一步延伸推导出体积流量的表达式。由于质量和体积之间相差一个密度,类比可知质量流量和体积流量之间也相差一个密度,所以只需用质量流量除以流体密度,就可以得到体积流量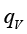 的表达式:
的表达式:
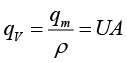 (1-3)
(1-3)
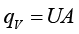 (1-4)
(1-4)
式(1-4)就是体积流量的表达式。因为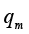 的单位为kg/s,
的单位为kg/s,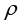 的单位为kg/m3,所以体积流量
的单位为kg/m3,所以体积流量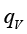 的单位为m3/s。
的单位为m3/s。
为什么要引入质量流量和体积流量的概念呢?因为自然界中的流体更多时候是处于流动状态的,与时间动态相关。在流体力学中我们更关注单位时间的质量和单位时间的体积,即质量流量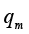 和体积流量
和体积流量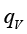 ,而不像固体力学那样关注总质量m和总体积V,这是流体力学和固体力学的区别。
,而不像固体力学那样关注总质量m和总体积V,这是流体力学和固体力学的区别。
对于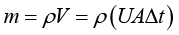 ,我们需要联想到如果把密度
,我们需要联想到如果把密度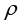 去掉,就可以得到
去掉,就可以得到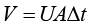 ,这就把面积
,这就把面积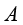 和体积
和体积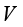 联系起来了,这也是在为我们后面要讲的高斯定理做铺垫——针对流体,面积和体积之间可以来回切换。
联系起来了,这也是在为我们后面要讲的高斯定理做铺垫——针对流体,面积和体积之间可以来回切换。
在正式推导连续性方程之前,我们还要回忆大一学过的泰勒展开,如图1-3所示。
一句话描述泰勒展开——用函数在某点的值来近似表示其附近点的值。我们先来回忆初中的知识:如图1-3(A)所示,当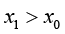 时,在直线
时,在直线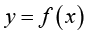 上取两个点
上取两个点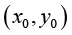 和
和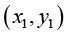 ,现在已知
,现在已知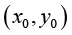 和
和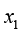 的值,想要求
的值,想要求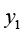 ,用初中数学知识,有
,用初中数学知识,有
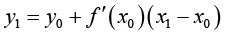 (1-5)
(1-5)
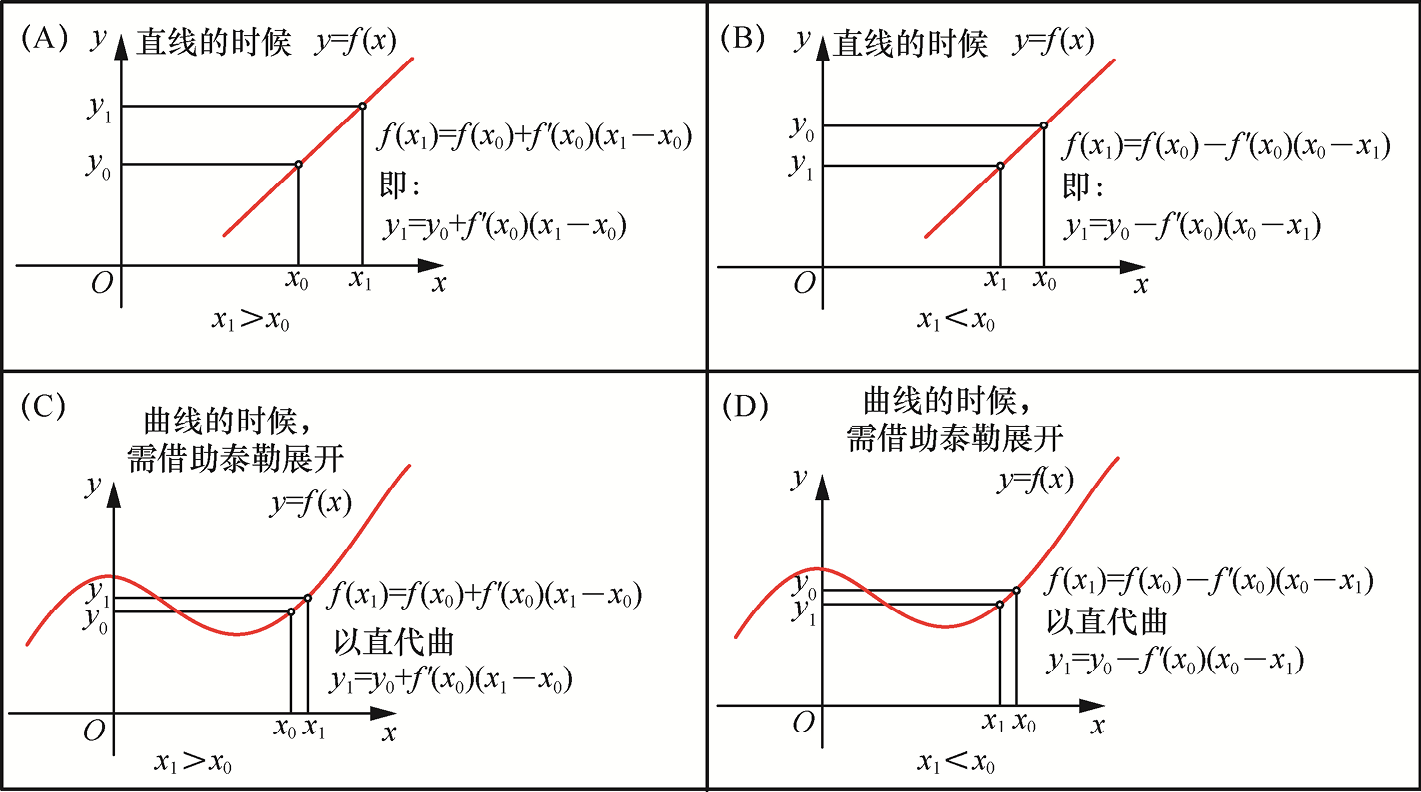
图1-3 泰勒展开示意图
如图1-3(B)所示,当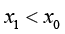 时,在直线
时,在直线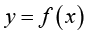 上取两个点
上取两个点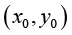 和
和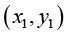 ,依旧已知
,依旧已知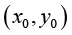 和
和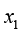 的值,想要求
的值,想要求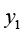 ,用初中数学知识,有
,用初中数学知识,有
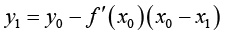 (1-6)
(1-6)
图1-3(A)~(B)都是直线问题,大家都会求。但如果是曲线,如图1-3(C)~(D)所示,依旧已知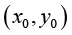 和
和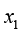 的值,想要求
的值,想要求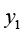 ,你还会求吗?这就要用到泰勒展开了,任何一个连续函数都可以用多项式近似。
,你还会求吗?这就要用到泰勒展开了,任何一个连续函数都可以用多项式近似。
针对图1-3(C),我们可以写出用点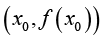 和
和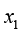 表示的
表示的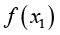 ,即
,即
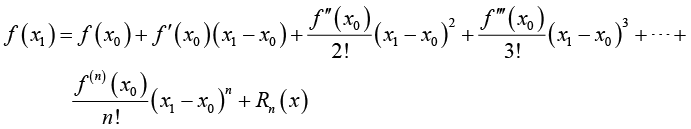
(1-7)
针对上式,如果我们只取前3项,把后面的项省略,会得到
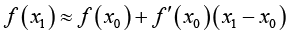 (这里采用约等号) (1-8)
(这里采用约等号) (1-8)
当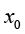 和
和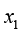 之间的距离非常短时,我们就认为
之间的距离非常短时,我们就认为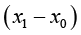 的值趋近于零,对于更高次幂
的值趋近于零,对于更高次幂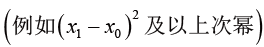 ,其值更加趋近于零,一般保留一次幂就满足工程需要了,所以可以把约等号化成直等号,即
,其值更加趋近于零,一般保留一次幂就满足工程需要了,所以可以把约等号化成直等号,即
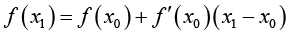 (这里采用直等号) (1-9)
(这里采用直等号) (1-9)
可以发现式(1-9)和图1-3(A)的式子相同。为什么会这样呢?因为x0和x1之间的距离非常短,故可以把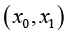 这段曲线当作直线来处理,即“以直代曲”。
这段曲线当作直线来处理,即“以直代曲”。
再来看图1-3(D),依旧是曲线,依旧套用泰勒展开,有
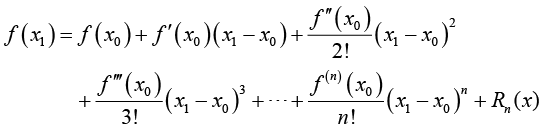 (1-10)
(1-10)
但因为此时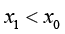 ,为了保证括号里面的差值为正值(因为默认距离取正),把
,为了保证括号里面的差值为正值(因为默认距离取正),把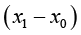 改成
改成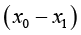 ,现在的泰勒公式变成了
,现在的泰勒公式变成了
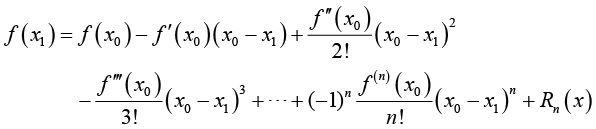 (1-11)
(1-11)
同样地,如果只取前3项,把后面的项都省略,可得
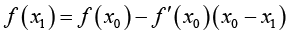 (1-12)
(1-12)
庄子与惠子游于濠梁之上。庄子曰:“鯈(tiáo)鱼出游从容,是鱼之乐也。”惠子曰:“子非鱼,安知鱼之乐?”庄子曰:“子非我,安知我不知鱼之乐?”
——《庄子·秋水》
这段古文想必很多朋友都看过,庄子和惠子站在桥上观赏游鱼,庄子情不自禁感叹鱼儿的自由。今天我们要从庄子赏鱼引申出流体力学中两种观测记录流体运动变化的方法,一种是欧拉法,另一种是拉格朗日法。为了帮助大家理解,假设此刻我们化身庄子,站在桥上看鱼,把鱼儿当作流体微元。如图1-4(A)所示,我们固定一个小框,通过观察这个小框内鱼儿(流体微元)的游动变化情况,判断流体的运动情况,这就是欧拉法,即我们站在桥上看框内鱼儿的游动情况,小框是固定不动的。
那什么是拉格朗日法呢?如图1-4(B)所示,我们选中一条锦鲤,给它的眼睛处加了一个点。此刻我们不再站在桥上看鱼儿流动了,而是想象将自己化身成一条鱼,在鱼儿的角度来观察流体的运动情况。拉格朗日法是在鱼儿的角度来观察流体的运动情况,鱼儿是可以四处游动的,并不是固定不动的。
综上:欧拉法是固定微团来观察微团内流体微元的变化,参见图1-4(C);而拉格朗日法是站在流体微团的角度来观察流体的变化,参见图1-4(D)。
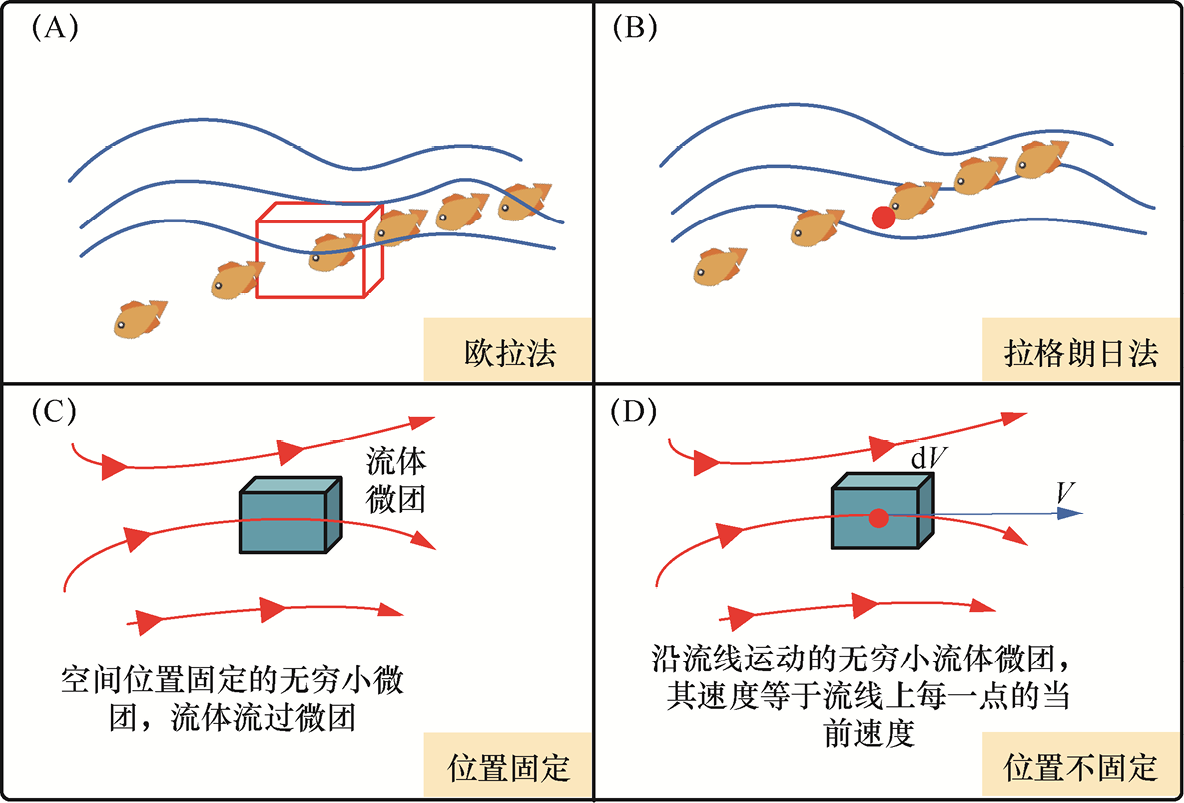
图1-4 鱼之乐之欧拉法与拉格朗日法
虽然都是描述流体的变化,但站在不同的角度看问题,最后得到的方程形式会有所不同。在CFD中,把采用欧拉法得到的微分方程称为守恒型方程,把采用拉格朗日法得到的微分方程称为非守恒型方程。记住,欧拉法和拉格朗日法是对同一事物(流体)的不同描述方法,它们在本质上是相同的,是可以互换的。有了这些预备知识,在第2章中我们就可以推导流体满足的控制方程,以及对流体控制方程的性质进行探讨了。