
书名:速通!深度学习的数学基础
ISBN:978-7-115-65002-3
本书由人民邮电出版社发行数字版。版权所有,侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用,未经授权,不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟,与我们共同保护知识产权。
如果购买者有侵权行为,我们可能对该用户实施包括但不限于关闭该帐号等维权措施,并可能追究法律责任。
著 [日]赤石雅典
译 张 诚
责任编辑 韩 松
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
网址 http://www.ptpress.com.cn
读者服务热线:(010)81055410
反盗版热线:(010)81055315
SAITAN COURSE DE WAKARU EEP LEARNING NO SUGAKU written by Masanori Akaishi.
Copyright 2018 by Masanori Akaishi. All rights reserved.
Originally published in Japan by Nikkei Business Publications, Inc.
Simplified Chinese translation published in 2025 by Posts & Telecom Press Co.,LTD.
本书将深度学习涉及的数学领域缩小到最小范围,以帮助读者在最短的时间内理解与深度学习有关的数学知识。全书分为导入篇、理论篇、实践篇和发展篇4篇。导入篇系统介绍一些机器学习的入门知识;理论篇包括微积分、向量和矩阵、多元函数、指数函数、概率论等知识;实践篇介绍线性回归模型、逻辑回归模型、深度学习模型;发展篇介绍面向实践的深度学习。本书编程实践中的代码使用Python及Jupyter Notebook编写,简明易懂,便于读者上手实践。
本书适合对深度学习感兴趣的读者、希望通过了解数学基础来学习深度学习的读者阅读。
本章结构
本书的目标是“通过数学来理解机器学习和深度学习”。
本章中,我们将用高中数学知识,通过清晰易懂的例子,来说明“到底什么是机器学习和深度学习”和“为什么机器学习和深度学习中非用数学不可”。
所谓人工智能(AI)与机器学习嘛……虽说我们老是听说,但如果问起定义,你能立刻答上来吗?
关于人工智能,据笔者所知还没有通用、明确、严密的定义。如果问起“什么是人工智能”,那一定是众说纷纭。从1950年开始,也就是设计“图灵测试[1]”的阿兰·图灵那个时代,人们就试图回答这个问题。实践中也将其称为“规则库系统[2]”,它包含基于知识数据推演来发现答案的方式。不得不说,人工智能这个词表达的范围非常广泛。
[1] 定义:人与隔离的房间里的计算机系统对话,如果无法判断对方是人还是计算机,则这个系统就是“人工智能”。(本书中未注明译者注的脚注均为作者原注。)
[2] 历史上最有名的规则库系统是20世纪70年代开发的名为MYCIN的系统。此系统基于已有知识,通过500条左右的规则来诊断患者的血液病类型,开出抗生素的处方。据说诊断的正确率达65%,虽不如专家,但比普通医生更精确。
与此相对,机器学习所指的内容和操作很明确,一定程度上可以严格定义。本书讨论的内容就是“机器学习”这个概念的内涵。
因此,本书原则上不使用“人工智能”这个词,而代之以“机器学习”来表达,将“深度学习”当作一种特定的“机器学习”的名字即可。至于是怎么个特定法,本章的后半部分会说明。
那么,机器学习到底是什么呢?虽然机器学习所指的东西是很明确的,但是表述的方法因人而异。为了统一认识,以下按照笔者的思路简单说明一下机器学习的定义。
本书定义的机器学习模型为满足以下两个原则的系统。
原则1:机器学习模型是对输入数据执行函数输出结果的模型。
原则2:机器学习模型的操作是通过学习得来的。
下面我们举例说明。请看表1-1的鸢尾花数据集,它是从机器学习中经常使用的公开数据抽取特定行、列的关于鸢尾花瓣尺寸的数据。class表示花的品种,length表示花瓣的长度,width表示花瓣的宽度。
表1-1 2种鸢尾花瓣的尺寸
| class |
length/cm |
width/cm |
|---|---|---|
| 0 |
1.4 |
0.2 |
| 1 |
4.7 |
1.4 |
| 0 |
1.3 |
0.2 |
| 1 |
4.9 |
1.5 |
| 0 |
1.4 |
0.2 |
| 1 |
4.9 |
1.5 |
这里我们考虑构建模型,只要输入length和width的值,就能输出品种的名字class。我们先人工观察一下表1-1中的6个数据。
只要实现这样的逻辑,我们就可以构造出一个能正确运转的黑箱。
但是,上述根据条件做判断的场景里有人参与,所以不是机器学习。既然是机器学习模型,人只要给模型输入数据就可以了,上述程序里条件的判断标准必须由模型自己发现,也就是前文第2条原则“操作是通过学习得来的”的意思。
机器学习模型必须学习,具体来讲有3种方法。
这种方法在给模型输入用于学习的数据时也输入对应的真实值(即有标签的数据)。
这种方法在输入学习的数据时,没有真实值,让模型自己学出点什么。根据样本数据自动分类的聚类分析就是无监督学习的代表。
这是一种介于监督与无监督学习之间的学习法。外部对模型输入观测值,模型根据所谓策略来行动,然后外部给出反馈。模型在输入步骤尚不知道真实值是什么,但后面通过收益就理解了真实值是什么。
以上三种学习方法中,监督学习的原理最简单易懂。本书介绍的便是监督学习。
举例来说,预测商店一天销售收入的数值,根据照片判断动物种类的离散值(称为“类别”或“标签”),都是监督学习模型。我们把前者称为回归模型,后者称为分类模型,如图1-1所示。本书中对回归模型与分类模型都有介绍。
图1-1 回归模型与分类模型
监督学习中,有“训练步”与“预测步”两个步骤。
训练步如图1-2所示,我们把样本数据与真实值(标签)作为训练数据输入,构造尽可能精确(预测结果与真实值接近)的模型。
图1-2 训练步
预测步里我们只输入样本数据,不带真实值(见图1-3)。机器学习模型用来预测输入样本的真实值是什么,并将其作为系统的输出。
图1-3 预测步
以上介绍的机器学习模型定义里,并不涉及内部结构,总之机器学习模型是个黑箱,根据外部输入来操作输出。要实现这样的功能,方法多种多样。例如有种分类模型叫作决策树,就是观察数据,自动做出if then else的规则,很近似人的思考方法。
但是,本书涉及的模型完全不同,其结构中自带参数,需要做函数的数值计算。因此,我们要以输出为目标,来调整模型中函数的参数。
利用损失函数学习的方法如图1-4所示。
图1-4 利用损失函数学习的方法
损失函数是表示模型的预测值与真实值(标签)相近程度的指标。两者相差越大,函数值越大。如果对于全部训练数据有yp = yt(预测值=真实值),损失函数值就是零。
“梯度下降法”是为了使损失函数值最小,调节模型的参数到最优的算法。
简而言之,这部分的目标就是帮助你理解“损失函数”与“梯度下降法”的思想。现在,光看上面的说明,你可能还是一头雾水,不过一点一点就能懂了。现在请把这两个词和图1-4都记住吧。
我们来举个简单的例题,使你对上一节所说的“损失函数”有个更具体的印象。虽然用“偏微分”推导更省时间,但是本书完全不使用高等数学知识,只需要用高中二次函数之类的数学知识即可说明。读了一遍之后,你就有了“使用基础数学知识来解机器学习模型”的印象。最好继续努力,争取能自己推导出来。
一元回归就是输入一个实数值(x),用模型来预测另一个实数值(y)。比如,输入成年男子的身高(cm),输出体重(kg)。模型的结构叫作“线性回归”。
线性回归是一次函数的预测模型,输入数据记作x,输出数据记作y,线性回归的预测表达式如下。[3]
[3] 通常,一次函数表达为y=ax+b,在机器学习里,a和b称为“权重”,大多用单词weight的缩写表示(如w0,w1),本书也沿用。
y=w0+w1x (1.3.1)
请看表1-2中的前3个样本。
表1-2 学习样本1
| 身高x/cm |
体重y/kg |
|---|---|
| 167 |
62 |
| 170 |
65 |
| 172 |
67 |
事实上,由于在数据上做了手脚,可以很容易地得出公式:
那么,表1-3中的5个样本又如何呢?
表1-3 学习样本2
| 身高x/cm |
体重y/kg |
|---|---|
| 166 |
58.7 |
| 176 |
75.7 |
| 171 |
62.1 |
| 173 |
70.4 |
| 169 |
60.1 |
随着这样的样本数的增加,谁也不知道预测表达式会成什么样子。我们必须用数学方法来解决问题。
首先,把表1-3中的样本用散点图表示出来(图1-5)。
图1-5 学习样本的2维散点图
图1-6中,我们画出了一条参数与模型预测值[4]关系的直线。
[4] 我们还没说预测值的求法。这里的参数值与预测值是暂定的。
图1-6 实际值与预测值的误差图
yt是真实值,yp是模型的预测值,回归模型的误差就是(yt−yp),相当于图1-6中的灰色线段。但是,多点的误差有正有负互相抵消,这如何是好?我们考虑把样本的真实值yt与预测值yp的差做二次方,再对所有点求和作为损失函数来评价。[5]
[5] 解决负值还有一个方法,就是用误差的绝对值,但是这样就没法做微分了,所以实际操作中不使用。
这种思路叫作“残差平方和”,它就是线性回归模型的标准损失函数。
现在损失函数是什么样子的呢?我们来实际计算一下。预测值用yp表示,从式(1.3.1)得到
我们把5个样本点的坐标表示为(x(i), y(i)),其中右上角的数字用来区别不同样本点。这样,损失函数L(w0, w1)就成了下式。
把上式展开,对w0、w1进行整理,得到下式。
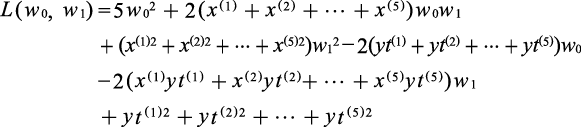 (1.3.2)
(1.3.2)
式(1.3.2)是关于w0、w1的二次式。这个式子里w0w1和w0的系数只与输入样本的x坐标和y坐标有关。然后,我们建立新坐标系,并把原样本点坐标值的平均值当作新原点建立新坐标系,如图1-7所示。
图1-7 原点的移动
我们来实际计算一下。x坐标的平均值是171.0,y坐标的平均值是65.4,用X、Y表示样本坐标减去它们后得到新的学习样本(表1-4)。
表1-4 学习样本3
| X |
Y |
|---|---|
| −5 |
−6.7 |
| 5 |
10.3 |
| 0 |
−3.3 |
| 2 |
5.0 |
| −2 |
−5.3 |
在新坐标系上做散点图,如图1-8。
图1-8 新坐标系上的散点图
新坐标系上的权重记作W0、W1,预测式变成如下式子。
 (1.3.3)
(1.3.3)
把新坐标系里的表1-4的X、Y值代入式(1.3.3),具体计算损失函数如下[6]。
[6] 具体而言,相当于与式(1.3.2)对应,把x和yt用新坐标系中的X、Yt来计算。
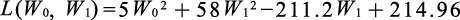 (1.3.4)
(1.3.4)
与W0有关的项只有5W02。这部分在W0=0时取最小值0。我们把剩余的58W12−211.2W1+214.96看成W1的二次函数,用配方法来求出最小值。
据此,我们知道当W1=1.82068...时函数取最小值为22.6951...。图1-9为L(0,W1)的函数的图像。
图1-9 L(0,W1)的图像
由此,我们就能得到损失函数(1.3.4)在新坐标系里取最小值的点,即
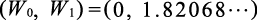 (1.3.5)
(1.3.5)
前一节提到,“训练步”“预测步”中,“训练步”的目的是计算最佳W0, W1。接下来开始讨论“预测步”。
把前面式(1.3.5)得到的参数值代入式(1.3.3),得到下式。
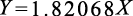 (1.3.6)
(1.3.6)
这就是本次计算得到的回归模型的预测公式。在原来的散点图里叠加上这条回归直线得到图1-10。
图1-10 散点图与回归直线(坐标系变换后)
可以看出这5个点可用直线近似拟合。最后再把坐标系移回原坐标系,得出原问题对应的回归模型预测公式。
可得
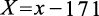 (1.3.7)
(1.3.7)
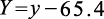 (1.3.8)
(1.3.8)
把式(1.3.7)和式(1.3.8)代入式(1.3.6),得到下式
把这个函数图像叠加到原来的散点图上,就有了一条拟合直线,如图1-11所示。这个模型叫作一元线性回归,它是机器学习里最简单的模型,只需高中数学知识就可以理解了。
图1-11 原坐标系上的散点图与预测公式函数图像
前一节中谈的是预测数值类型的回归模型,但本书最终目的是深度学习,多为预测离散值类型的分类模型。尽管如此,这里我们先介绍回归模型,是因为它在数学上很优美,理解它可以更容易地理解分类模型。
实现分类功能的模型各种各样,表1-5总结了其中的典型模型。
表1-5 典型分类模型
| 模型名 |
概要 |
|---|---|
| 逻辑回归 |
线性回归叠加上Sigmoid函数来表达概率 |
| 神经网络 |
在逻辑回归上叠加隐藏层 |
| 支持向量机 |
使二元分类样本值与间隔边界的距离最大化 |
| 朴素贝叶斯 |
用贝叶斯公式根据观察值来更新概率 |
| 决策树 |
把特征按阈值分类 |
| 随机森林 |
使用多棵决策树分类 |
本书从这些分类模型中选了“逻辑回归”和“神经网络”作特别介绍。这两种模型有相通点,然后本书的最终目标“深度学习”就是这两种模型的进阶版。
我把“逻辑回归”“神经网络”“深度学习”的共同特点整理如下,可列为(A)到(E)。
(A)模型的结构是事先确定的,只有参数能自由调节。
(B)构建模型过程如下:
(1)将各输入值乘以参数(称为“权重”);
(2)对乘积求和;
(3)把(2)的结果输入函数(称为“激活函数”),输出作为最终的预测值(yp)。
(C)通过学习将参数(权重)最优化。
(D)用“损失函数”来判断模型对真实值预测的准确度。
(E)用“梯度下降法”来获取损失函数中的合适参数。
图1-12所示为(B)的模型结构。
图1-12 预测模型的结构
逻辑回归是指具有一层图1-12结构的模型。神经网络中,在其中间加了一个“隐藏层”,形成两层的结构(图1-13)。
图1-13 神经网络模型的结构
具有三层以上(含两层隐藏层以上)的学习模型一般叫作深度学习模型。这里的三个模型层数不同,预测、学习的方式基本相同。[7]
[7] 之所以叫“神经网络”,是因为它是以大脑中神经细胞的生物学结构为基础来考虑的数学模型。“层”的结构对应神经细胞,只有“输入层”“输出层”之间细胞直接相连的模型是“逻辑回归”,在“输入层”“隐藏层”“输出层”间有两段层间细胞相连的模型是“神经网络”,包含两个以上“隐藏层”、有3段以上层间细胞相连的复杂结构模型叫作“深度学习”。
其实前文介绍的所谓“线性回归”模型,不是分类模型,而是回归模型,但它与现在介绍的分类模型非常相似,只不过缺少(B)-(3)的激活函数,此外从(A)到(D)全都满足。(图1-14[8])
[8] 关于(E),虽然使用“梯度下降法”是可以解题的,但是涉及的数学比较难,所以前文在高中数学知识范围内使用了配方法求解。
也就是说,仅从预测公式的结构来看,线性回归模型可算是逻辑回归系列分类模型的前置。
图1-14 线性回归模型的结构
这些内容在本书后面的实践篇开头的线性回归模型里都有,此后是分类模型的逻辑回归模型、神经网络,进一步延拓为深度学习。我想以这样方式介绍机器学习模型的进化历程。
本书的实践篇以分类模型为中心,以损失函数为线索,求解最优参数,使用的是1.3节说明的回归模型的基本思想。
1.3节中的模型是一次函数和二次函数,但是之后的预测函数和损失函数形如下式,这使得运算理解难度大大提高。
[exp (x)是以自然常数为底的指数函数]
(lnx是以自然常数为底的对数函数)
对于自然常数是什么,指数函数和对数函数又是什么,微分什么样,如果掌握的数学知识量还不到高三的水平,那还真是束手无策。然后,即使是比分类模型简单的线性回归模型,也有不只用身高,还加上胸围等数据精确地预测体重的多元回归模型。对于这种模型,1.3节中介绍的“平移坐标系→二次函数的平方法”这种高一水平的解题方法就搞不定了。至少,多元函数中的偏微分的概念必不可少。
无论如何,如果我们想要理解线性回归和逻辑回归系列的机器学习模型,就必须保证对数学理解到一定程度。更何况,如果想理解进阶版的深度学习模型,数学就更必要了。
前文讲了数学的必要性,本书是理解深度学习的捷径。我在理论篇里介绍了最低限度需要掌握的数学概念。在实践篇里,使用理论篇介绍的数学知识,高效地学习机器学习和深度学习的精华。
各部分的详细结构如下。本书的结构在插页里面,请在阅读过程中随时回顾。
理论篇里我将要介绍的是数学的理论体系,也包括数学的演进、深度学习必要的数学概念和公式。这一部分会包含大学程度的内容,以高中生的数学水平也能理解大部分。本书里我选取机器学习和深度学习必要的概念,建立分析体系,使大家尽可能地理解这些概念。
在此目标下,我删掉了很多一般教科书里写的内容(例如三角函数的微分、逆矩阵、特征值、特征向量等)。请看好,本书是直奔目的地去的。
图1-15是理论篇全体概念之间的关系。第2章“微分与积分”与第3章“向量与矩阵”相互独立,但是第4章及以后都依赖这两章。
图1-15 理论篇的结构
图1-16 ~图1-20表示各章内部概念之间的关系。有“学习重点”标记的方框在实践篇里会直接使用,是实现深度学习必需的概念。另外,灰色方框表示这是非常重要的概念,所以请好好理解。对基础部分已经大体了解的读者,如果阅读重要的部分时有不明白的,也可以沿着这个图追溯不明白的部分。
图1-16 第2章概念之间的关系
图1-17 第3章概念之间的关系
图1-18 第4章概念之间的关系
图1-19 第5章概念之间的关系
图1-20 第6章概念之间的关系
在实践篇里,我会按章出例题,沿着主题循序渐进,学习机器学习算法和实现代码。每个主题后面的章节包含很难的内容。
我画了表1-6来对应理论篇里阐述的“必需”的各种概念。第10章里就是我们一直期望掌握的深度学习了。从表中可知,第9章的多分类与第10章的深度学习在必需的概念上几乎没有区别。请一章一章阅读,一步一步前行,总能到达“深度学习”的山顶。
实践篇里,我坚持“码码致知”的原则。各章的最后一节都会附上代码。
在实践里,我们会最大限度地活用NumPy[9]的特点,目标是“无循环编程”。一实践操作,就能轻易读懂各算法的核心,也容易明白各算法的结构。对于实操必需的NumPy技术,在必要的地方我都有解说。
[9] NumPy是Python中做数值运算的模块,特别适合向量和矩阵计算,是用Python做机器学习和深度学习编程的必需模块。
表1-6 必需的数学概念与机器学习和深度学习的关系
从下一章开始我们就要进入理论篇了。因为设定是从高一的数学水平开始,只要花工夫详细阅读,一定可以融会贯通。虽然包含了部分稍微有难度的叙述,但为了理解深度学习那也必不可少。请抱有这种意识前进吧。