

书名:扩散模型 核心原理与强化学习优化
ISBN:978-7-115-67612-2
本书由人民邮电出版社发行数字版。版权所有,侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用,未经授权,不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟,与我们共同保护知识产权。
如果购买者有侵权行为,我们可能对该用户实施包括但不限于关闭该帐号等维权措施,并可能追究法律责任。
著 陈 云 牛雅哲 张金欧文
责任编辑 武少波
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
网址 http://www.ptpress.com.cn
读者服务热线:(010)81055410
反盗版热线:(010)81055315
本书通过系统化的理论讲解与实战导向的案例分析,帮助读者掌握扩散模型与强化学习的结合应用,探索其针对实际问题的解决方案。书中首先介绍了生成模型的发展史,特别是扩散模型的起源和核心思想,为读者学习后续章节奠定基础;然后深入探讨了扩散模型在构建决策智能体、结合价值函数等方面的应用,还详细讲解了如何利用扩散模型解决轨迹优化和策略优化等问题;接下来探索了扩散模型在多任务泛化和世界模型建模方面的扩展应用,展示了其在复杂环境中的适应性和灵活性;最后讨论了利用强化学习优化扩散模型的新进展,以及扩散模型在决策问题上的前沿研究方向。
通过本书的学习,读者不仅能够理解扩散模型和强化学习的理论基础,还能掌握将其应用于实际问题的技巧和方法。无论你是人工智能领域的研究者,还是希望在实际项目中应用这些技术的工程师,本书都将为你提供有价值的参考和指导。
生成式人工智能技术正以前所未有的发展速度推动学科前沿和实际应用的革新浪潮。其中,扩散模型(Diffusion Model)在深度学习、自然语言处理、图像生成、强化学习等领域展现出卓越的能力和灵活性。不同于以往生成模型单纯的“捕捉数据分布”工作方式,扩散模型以独到的“逐步加噪/去噪”机制,实现了对复杂高维数据的逼真合成与创新变换,成为生成建模领域的“明星技术”。
与此同时,强化学习和智能决策技术也在不断突破理论与应用的边界。在机器学习、机器人控制、自动驾驶、元学习等复杂任务中,如何高效地利用离线数据进行学习、如何实现多任务的泛化能力,成为业界与学界关注的核心难题。近年来,关于扩散模型与强化学习深度融合的研究不断涌现:将扩散模型视作通用策略分布建模工具、将强化学习引入扩散模型的目标优化乃至构建具备泛化能力的“世界模型”……一系列创新性框架极大丰富了人工智能的研究和应用内涵。
这本书,既是作者多年参与深度应用扩散模型、强化学习和生成建模相关工作的总结,也是作者就阅读、学习和实践过程中所产生的各种疑问和困惑的自我回应。尽管扩散模型的相关研究和应用突飞猛进,但国内系统梳理“扩散模型+智能决策/强化学习”相关主题的图书等学习资料依然匮乏。许多有志于深入生成建模与智能决策一线的学习者,在面对工程难题时,仅靠庞杂的论文、碎片化的教程,很难快速构建完整的知识脉络和实践路径。
与其说本书是作者总结近年来的所学、所思与所得,不如说是为更多正在学习、探索和奋斗于人工智能前沿的同行铺就了一条相对平整的路,使大家能够得到更多启发,少走弯路。诚挚希望每一位读者,不仅能在书中找到技术解答,而且能体会到创新的乐趣和学以致用的成就感,并对人工智能未来的无限可能充满信心。
本书内容分为多个层次,从理论基础到算法实践,从模型设计到多领域应用,覆盖了扩散模型的“全技术脉络”。
● 全面梳理生成模型的发展史,包括早期的概率模型、变分自编码器(Variational Auto-Encoder,VAE)、生成对抗网络(Generative Adversarial Network,GAN)、扩散模型等范式,为读者勾画出技术演进的背景。
● 系统阐述扩散模型的数学机制,其中涉及加噪/去噪过程、数学原理、训练方法、条件采样与加速采样方法等关键技术环节。
● 深入介绍扩散模型在强化学习与决策问题中的开创性应用,如轨迹优化与离线强化学习、与价值函数结合的Diffusion-QL、CEP/QGPO、LDCQ等算法,剖析其创新点与实际效果。
● 探讨扩散模型在多任务泛化、世界模型建模(如基于RNN/Transformer/扩散模型的世界模型框架)以及机器人控制、自动驾驶、高维数据分布建模等复杂场景下的前沿进展与瓶颈。
● 展示如何反向利用强化学习算法优化扩散模型,推动生成模型与人类偏好的深度对齐与目标导向进化。
● 提供大量贴合实际的代码实例、算法流程与实验配置,便于读者将理论知识应用到具体工程实践和研究探索之中。
本书在内容设计和表达方式上具有如下鲜明特色。
● 理论与工程兼顾:既重视数理基础和方法体系,又紧密结合算法实现、实验评测与应用案例,帮助读者形成“原理—实现—系统”的全景认知。
● 前沿交叉、脉络明晰:全书紧跟最新学术进展,系统梳理扩散模型与强化学习、世界模型等领域的交叉创新成果,构筑体系化的技术脉络。
● 示例丰富、直观易懂:提供足够多的代码、伪代码与实验配置,辅以丰富的可视化示意图,并采用多种对比手法进行讲解,力求让复杂原理与算法一目了然、易于上手。
● 注重应用与未来展望:不仅解析现有成果的优势与局限,也对未来机器人、自动驾驶、智能体等领域的扩展潜力提出洞见与展望。
本书适合以下读者。
● 对生成模型、深度学习、决策优化、强化学习、机器人学等方向感兴趣的高校学生、研究人员。
● 从事AI系统开发、数据建模、算法研究等工作的产业工程师和产品经理。
● 关注人工智能前沿发展、希望深度理解并实践扩散模型与智能决策融合的学习者。
● 有一定机器学习/深度学习基础、希望系统提升工程和理论能力的相关从业者。
扩散模型处在人工智能技术新的风口,是数智世界构建与创新的重要推手。愿本书能够成为你探索生成模型前沿与复杂智能决策问题的有力助手,助你在这片“蓝海”中不断超越、突破自我!
陈云
2025年6月
本书提供如下资源:
● 配套代码文件;
● 本书思维导图;
● 异步社区7天VIP会员。
要获得以上资源,您可以扫描右侧二维码,根据指引领取。

作者和编辑尽最大努力来确保书中内容的准确性,但难免会存在疏漏。欢迎您将发现的问题反馈给我们,帮助我们提升图书的质量。
当您发现错误时,请登录异步社区(https://www.epubit.com),按书名搜索,进入本书页面,单击“发表勘误”,输入错误信息,单击“提交勘误”按钮即可(见下图)。本书的作者和编辑会对您提交的错误信息进行审核,确认并接受后,您将获赠异步社区的100积分。积分可用于在异步社区兑换优惠券、样书或奖品。
我们的联系邮箱是contact@epubit.com.cn。
如果您对本书有任何疑问或建议,请您发邮件给我们,并在邮件标题中注明本书书名,以便我们更高效地做出反馈。
如果您有兴趣出版图书、录制教学视频,或者参与图书翻译、技术审校等工作,可以发邮件给我们。
如果您所在的学校、培训机构或企业想批量购买本书或异步社区出版的其他图书,也可以发邮件给我们。
如果您在网上发现有针对异步社区出品图书的各种形式的盗版行为,包括对图书全部或部分内容的非授权传播,请您将怀疑有侵权行为的链接通过邮件发送给我们。您的这一举动是对作者权益的保护,也是我们持续为您提供有价值的内容的动力之源。
“异步社区”是由人民邮电出版社创办的IT专业图书社区,于2015年8月上线运营,致力于优质内容的出版和分享,为读者提供高品质的学习内容,为作译者提供专业的出版服务,实现作译者与读者在线交流互动,以及传统出版与数字出版的融合发展。
“异步图书”是异步社区策划出版的精品IT图书的品牌,依托于人民邮电出版社在计算机图书领域四十余年的发展与积淀。异步图书面向各行业的信息技术用户。
生成模型(Generative Model)是机器学习的一个重要分支,它的核心目标是从数据中学习其潜在结构,并生成与真实数据相似的新样本。生成模型的发展历程可以分为几个重要的阶段,每个阶段都推动了生成模型的能力提升与广泛应用。从早期的概率模型,到近年来深度学习的爆发式增长,再到多模态生成的前沿探索,生成模型正逐渐成为数据科学与人工智能领域的重要技术。以下是生成模型发展的历史演变。
生成模型的起源可以追溯到二十世纪八九十年代,当时许多概率模型为生成模型后来的发展奠定了基础。
隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model,HMM)是最早的生成模型之一,广泛应用于语音识别和自然语言处理(Natural Language Processing,NLP)等序列数据任务。HMM通过隐藏状态的序列,建模了观测数据的生成过程。其强大的序列建模能力使得HMM在早期成为生成模型的重要工具。
高斯混合模型
高斯混合模型(Gaussian Mixture Model,GMM)是另一种经典的生成模型,其通过多个高斯分布的线性组合来近似复杂的数据分布。GMM已广泛应用于聚类和模式识别任务,如语音信号处理和图像分割。它在解决非线性可分数据的问题上具有明显优势,是早期生成模型的代表之一。
随着计算能力的增强和数据量的爆炸式增长,深度学习逐渐成为主流,生成模型也随之进入新的发展阶段。
深度信念网络
深度信念网络(Deep Belief Network,DBN)[1]是由Geoffrey Hinton等人提出的生成模型,通过多层受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)堆叠而成。DBN的多层结构使得它能够从高维数据中提取有意义的特征,并且能够以无监督方式学习数据的隐含分布。
变分自编码器
变分自编码器(Variational Auto-Encoder,VAE)[2]是一种概率生成模型,它先通过编码器将数据映射到潜空间,再通过解码器生成新的数据样本。VAE不仅能够生成与输入数据相似的样本,还能够进行潜空间的连续操作,从而在生成过程中提供更大的灵活性和可解释性。VAE在图像和文本生成以及其他任务中表现出色。
GAN的提出
生成对抗网络(Generative Adversarial Network,GAN)[3]由Ian Goodfellow等人在2014年提出,它通过生成器和判别器的对抗性训练,使生成器能够产生逼真的样本。
GAN的提出标志着生成模型领域的一次革命性进展。GAN凭借其对抗训练的机制,显著提升了生成模型的质量和多样性。
GAN的工作原理如下:生成器试图生成与真实数据无法区分的新数据,而判别器则努力将真实数据与生成数据区分开来。通过这样的对抗训练,生成器不断改进,最终生成高质量的样本。
GAN的变体
随着时间的推移,研究人员提出了多种GAN的变体,以提升其生成能力和稳定性。例如,条件GAN(CGAN)引入了标签信息,使生成器能够生成特定类别的样本;深度卷积GAN(DCGAN)利用卷积神经网络提升了所生成图像的质量;风格GAN(StyleGAN)更是通过风格控制的方式,生成了高度细腻且控制精细的图像。这些GAN变体在图像生成、视频生成、超分辨率等领域取得显著的成果。
自回归模型通过逐个生成数据点的方式,成为生成模型中的重要一类,特别是在图像和文本生成领域表现出色。
PixelRNN/PixelCNN
PixelRNN和PixelCNN[4]是两种典型的自回归图像生成模型,它们通过逐个像素生成图像内容,确保生成的每个像素都依赖于之前的像素。这种逐像素生成的方式尽管计算开销较大,却能精确捕捉图像的局部结构和细节。
Transformer架构
Transformer架构最初用于NLP任务,后来也广泛应用于图像生成任务。OpenAI提出的DALL-E模型通过将Transformer架构应用于图像生成,来根据文本描述生成逼真的图像。同样,Google的Imagen也通过Transformer架构在生成任务中取得显著突破。
扩散模型是一种基于噪声添加与去噪的生成模型,近年来在图像生成领域取得巨大成功。
扩散概率模型
扩散概率模型通过逐步添加噪声将数据扰乱,然后通过学习逆过程生成清晰的图像。扩散概率模型的关键在于去噪过程的精确性和控制力,这使得它在高质量图像生成领域备受瞩目。OpenAI的DALL-E 2和Google的Imagen基于这种技术,能够生成极为精细的图像。
为了充分发挥不同生成模型的优势,研究人员开始探索多种技术的融合。
VAE-GAN
VAE-GAN是将VAE的概率解释性与GAN的高质量生成能力相结合的一种混合模型。这种混合模型能够同时利用VAE的潜空间结构和GAN的对抗性学习,从而生成更加多样化且逼真的数据。
多模态生成模型
随着数据形式变得多样化,生成模型逐渐向多模态领域扩展。例如,OpenAI提出的CLIP和DALL-E模型不仅能够理解文本与图像之间的关系,还能够根据文本描述生成图像。
多模态生成模型的出现标志着生成模型应用场景的进一步扩大,尤其是在跨领域数据生成与理解上展现出巨大的潜力。
生成模型从最早的统计学模型,到深度学习的蓬勃发展,再到近年来的多模态生成模型,经历了多次技术革命。每一次技术的进步都极大地拓宽了生成模型的应用范围。如今,生成模型不仅在学术研究中扮演着重要角色,更是在图像生成、内容创作、医疗健康等领域展现出广阔的应用前景。
扩散模型是一种将扩散过程(Diffusion Process)的逆过程(Inverse Process)作为其生成过程的流生成模型(Flow-based Generative Model)。
扩散过程在自然界中广泛存在,比如热量的传导、气体分子的布朗运动、溶液密度的变化,以及更广泛意义上,诸如人类社会中的知识、技术、观点、注意力的传播和平衡过程等。扩散的本质是任何一种事物从较高密度区域向较低密度区域的随机运动,可以描述为一种随机过程(Stochastic Process)。
从布朗运动的视角来看,如果在扩散过程中,空间中的每一个位置附近都存在足以满足统计规律的粒子,则它们的运动轨迹可以用如下随机微分方程来描述:
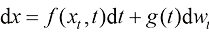 (1.1)
(1.1)
在式(1.1)中,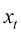 为粒子的位置,
为粒子的位置,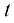 为时刻,
为时刻,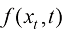 为xt 位置的粒子在t时刻的运动的漂移速度,
为xt 位置的粒子在t时刻的运动的漂移速度,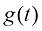 为t时刻的粒子的扩散系数,反映了t时刻的扩散程度,
为t时刻的粒子的扩散系数,反映了t时刻的扩散程度,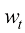 为一个标准维纳过程(Wiener Process)。
为一个标准维纳过程(Wiener Process)。
为了进一步简化运动轨迹的类型,仅考虑由线性随机微分方程控制的运动轨迹:
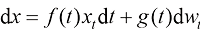 (1.2)
(1.2)
在式(1.2)中,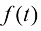 为t时刻的漂移系数。
为t时刻的漂移系数。
对于这类运动轨迹,从单一粒子的视角来看,在初始时刻,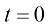 ,
,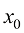 位置的粒子在未来某一时刻
位置的粒子在未来某一时刻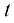 的位置
的位置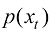 服从如下形式的高斯分布:
服从如下形式的高斯分布:
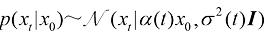 (1.3)
(1.3)
在式(1.3)中,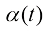 为t时刻的平均位置与初值位置之间的比例,称为比例(Scale)系数,
为t时刻的平均位置与初值位置之间的比例,称为比例(Scale)系数,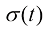 为t时刻的粒子位置的标准差。
为t时刻的粒子位置的标准差。
在拟定粒子运动方程的漂移系数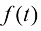 与扩散系数
与扩散系数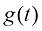 之后,它们的数值满足如下数学关系:
之后,它们的数值满足如下数学关系:
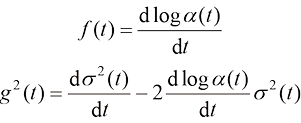 (1.4)
(1.4)
在每一个时刻,空间中全体粒子的分布可以视为一种概率分布。其概率密度函数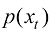 作为空间和时间的函数,可以由福克-普朗克-柯尔莫哥洛夫方程(Fokker-Planck Kolmogorov Equation)确定:
作为空间和时间的函数,可以由福克-普朗克-柯尔莫哥洛夫方程(Fokker-Planck Kolmogorov Equation)确定:
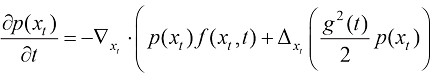 (1.5)
(1.5)
可以将式(1.5)转换为连续性方程(Continuity Equation)的形式:
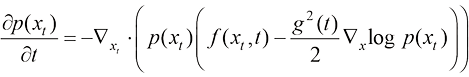 (1.6)
(1.6)
对于一个不存在掺混的粒子运动过程,它的流动过程可以用一个常微分方程来描述:
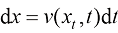 (1.7)
(1.7)
其粒子的平均速度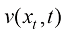 与每个粒子的漂移速度
与每个粒子的漂移速度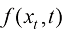 相同。因此,其连续性方程遵循:
相同。因此,其连续性方程遵循:
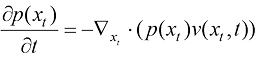 (1.8)
(1.8)
对于存在掺混的扩散过程,假设它与一个不存在掺混的粒子运动过程具有相同的概率密度分布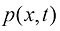 ,则这个不存在掺混的粒子运动过程的平均速度
,则这个不存在掺混的粒子运动过程的平均速度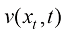 需要具有以下形式:
需要具有以下形式:
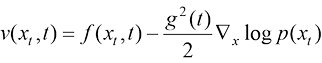 (1.9)
(1.9)
与此同时,我们可以将扩散过程的平均速度定义为上述形式。在式(1.9)中,概率密度函数的对数关于随机变量的梯度场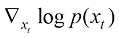 称为得分函数(Score Function)。
称为得分函数(Score Function)。
扩散的本质是将高密度分布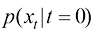 转换为某种低密度分布
转换为某种低密度分布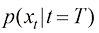 ,比如高斯分布
,比如高斯分布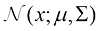 。保持扩散过程中每个时刻的整体概率密度分布不变,从时间维度逆转上述运动过程,即可通过扩散过程的逆过程,将某种低密度分布
。保持扩散过程中每个时刻的整体概率密度分布不变,从时间维度逆转上述运动过程,即可通过扩散过程的逆过程,将某种低密度分布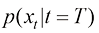 转换为高密度分布
转换为高密度分布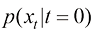 。
。
由此可见,扩散模型是一种将扩散过程的逆过程作为其生成过程的流生成模型。
我们可以将扩散模型建模为得分函数模型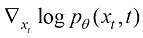 、速度模型
、速度模型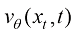 、噪声模型
、噪声模型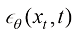 等任意多种形式,它们有如下变换关系:
等任意多种形式,它们有如下变换关系:
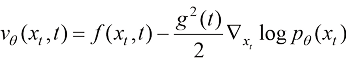 (1.10)
(1.10)
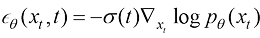 (1.11)
(1.11)
可以看到,由于每一个扩散模型都有一个确定的扩散过程与之对应,即数值确定的漂移速度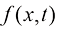 与扩散系数
与扩散系数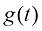 ,因此对于同一个数据集,不同建模方式的扩散模型的数学本质是等价的。
,因此对于同一个数据集,不同建模方式的扩散模型的数学本质是等价的。
生成模型的训练一般基于对数据集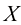 的最大似然估计(Maximum Likelihood Estimation,MLE)。假如模型的建模参数是
的最大似然估计(Maximum Likelihood Estimation,MLE)。假如模型的建模参数是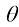 ,那么优化模型的目标为最大化
,那么优化模型的目标为最大化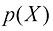 ,一般使用以下形式的目标方程来实现:
,一般使用以下形式的目标方程来实现:
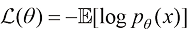 (1.12)
(1.12)
然而,对扩散模型直接使用上面的训练目标等价于训练一个连续正则化流(Continuous Normalizing Flow)模型,需要使用连续变量转换公式(Instantaneous Change of Variables Formula),积分和求解对数似然函数在流动过程中的变化量,且训练过程常常陷入不稳定的情形。而为了有效且稳定地训练,需要使用一系列正则化技巧,详见论文[5]“How to train your neural ODE:the world of Jacobian and kinetic regularization”。
为了规避这一点,扩散模型采用了一种以扩散过程的逆过程为固定生成过程的设计。当数据固定时,扩散过程的类型固定,扩散过程的逆过程虽然未知,但其存在且唯一。这样一来,扩散模型的训练就有了一个固定的监督学习目标,而不必直接计算对数似然函数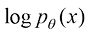 ,也不会受到不稳定的训练过程的干扰。恰恰相反,这样的训练目标非常稳定。具体来说,扩散模型的主流训练方法有两种,分别为得分匹配(Score Matching)算法与流匹配(Flow Matching)算法。
,也不会受到不稳定的训练过程的干扰。恰恰相反,这样的训练目标非常稳定。具体来说,扩散模型的主流训练方法有两种,分别为得分匹配(Score Matching)算法与流匹配(Flow Matching)算法。
得分匹配算法计算以下形式的训练目标函数,又称显式得分匹配(Explicit Score Matching)算法:
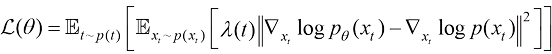 (1.13)
(1.13)
可以看到,得分匹配算法计算一个加权的均方差损失函数并将其作为扩散模型的训练目标函数。其中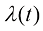 为不同类型的加权系数。在式(1.13)中,由于真实的得分函数
为不同类型的加权系数。在式(1.13)中,由于真实的得分函数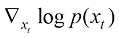 未知,因此无法直接计算。Pascal Vincent在论文[6]“A connection between score matching and denoising autoencoders”中提出了效果等价于显式得分匹配算法的降噪得分匹配(Denoising Score Matching)算法,形式如下:
未知,因此无法直接计算。Pascal Vincent在论文[6]“A connection between score matching and denoising autoencoders”中提出了效果等价于显式得分匹配算法的降噪得分匹配(Denoising Score Matching)算法,形式如下:
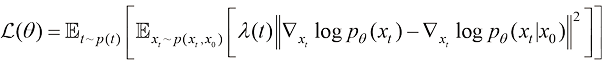
(1.14)
在式(1.14)中,条件得分函数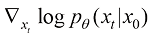 在扩散过程中是可解析的:
在扩散过程中是可解析的:
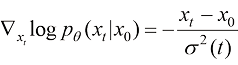 (1.15)
(1.15)
与得分匹配算法的思路相近,流匹配算法旨在监督训练模型的速度场,并计算以下形式的训练目标函数:
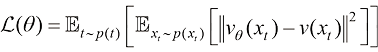 (1.16)
(1.16)
从式(1.16)中可以看到,流匹配算法一般不再引入随时间变化的加权系数,而希望全局一致地按照概率流的密度分布监督学习整个流场的速度。Yaron Lipman等人在论文[7]“Flow matching for generative modeling”中率先给出了以高斯分布为先验的流匹配算法,而后Alexander Tong等人在论文[8]“Improving and generalizing flow-based generative models with minibatch optimal transport”中将该算法推广到了可以将任意分布作为先验的更通用形式,称为条件流匹配(Conditional Flow Matching)算法:
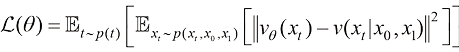 (1.17)
(1.17)
在式(1.17)中,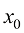 为来自先验分布
为来自先验分布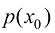 的样本,而
的样本,而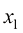 为来自数据分布
为来自数据分布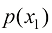 的样本。
的样本。
扩散模型的推断过程是对扩散过程的逆过程的演绎。逆向回溯扩散过程需要使用与正向过程拥有相同概率密度分布的某种逆过程。
可以直接使用由福克-普朗克-柯尔莫哥洛夫方程给定的常微分方程作为生成路径:
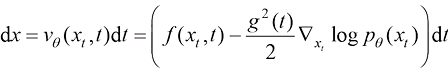 (1.18)
(1.18)
该常微分方程也称概率流常微分方程(Probability Flow ODE)。
也可以在逆向过程的生成路径中注入一定规模的高斯噪声,此时对应相同概率密度分布的逆向过程的生成路径可以使用一种随机微分过程来描述:
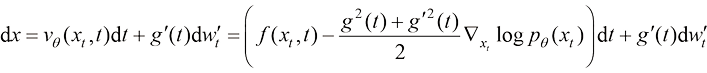
(1.19)
在式(1.19)中,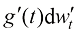 为采样过程中额外注入的高斯噪声,其幅值
为采样过程中额外注入的高斯噪声,其幅值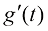 理论上不受任何限制,但一般可以选取和扩散过程的前向过程(又称前向扩散过程)相同的加噪方案,即
理论上不受任何限制,但一般可以选取和扩散过程的前向过程(又称前向扩散过程)相同的加噪方案,即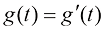 。此时,式(1.19)变化为
。此时,式(1.19)变化为
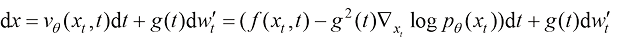
(1.20)
论文[9]“Elucidating the design space of diffusion-based generative models”详细论述了在生成过程中额外注入高斯噪声所带来的效果及其机制。如果扩散模型的建模和训练是理想的,则理论上使用任意一种生成路径所得到的采样分布将是一致且有效的。但在具体实践中,扩散模型的建模不可能是完美的,训练无法完全做到收敛和正确,在生成过程中注入噪声等价于破坏前期生成路径中的相关信息,从而后期必须在生成路径中使用更强的来自得分函数的引导。假如前期生成路径的得分函数训练不充分,而后期生成路径的得分函数训练充分,则在生成过程中添加一定的噪声可以有效地纠正生成路径。
扩散模型作为一种生成模型,隐式地建模了数据的概率分布,因此具备评估生成结果的概率密度的能力。为了在数值上易于分析,我们将其表示为负对数似然(Negative Log-Likelihood,NLL),并以每维度比特作为计量单位:
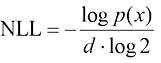 (1.21)
(1.21)
一个已训练的扩散模型的似然函数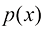 可以使用瞬时变量变换定理(Instantaneous Change of Variable Theorem)来计算:
可以使用瞬时变量变换定理(Instantaneous Change of Variable Theorem)来计算:
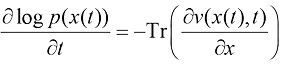 (1.22)
(1.22)
对式(1.22)进行定积分,可以得到:
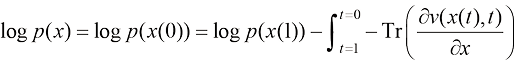 (1.23)
(1.23)
除了负对数似然之外,扩散模型也可以从生成质量的效果来评价。对于输出对象为图像的扩散模型,可以使用计算机视觉(Computer Vision,CV)领域的通用评价指标,比如FID(Frechet Inception Distance)与IS(Inception Score)。它们是基于Google的预训练网络Inception Net-V3进行相关生成质量评估的指标。在强化学习领域,当使用扩散模型建模策略函数时,可以直接通过该策略在评估场景时的总回报,来评估扩散模型的训练质量。
虽然所有的扩散模型都使用同一个定义式,但不同扩散模型具体的加噪方式与构造形式不同。我们可以通过安排不同形式的比例系数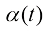 和噪声方差
和噪声方差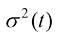 来确定具体的扩散轨迹。
来确定具体的扩散轨迹。
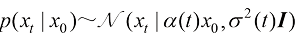 (1.24)
(1.24)
只需要满足式(1.24)即可。换言之,只需要满足当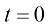 时
时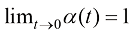 且
且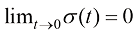 ,以及当
,以及当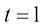 时
时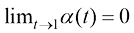 的边界条件即可。
的边界条件即可。
对于扩散模型,比例系数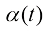 和噪声方差
和噪声方差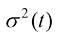 与漂移系数
与漂移系数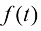 和扩散系数
和扩散系数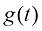 之间存在确定的数学关系:
之间存在确定的数学关系:
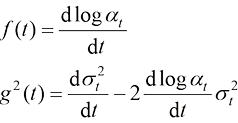 (1.25)
(1.25)
连续时间扩散模型
连续时间扩散模型一般将扩散过程设定在[0,1]连续区间,并让其训练和推断在整个连续区间内进行。
常见的连续时间扩散模型及对应系数如表1.1所示。
表1.1 常见的连续时间扩散模型及对应系数
| 连续时间扩散模型 |
对应系数 |
|
|---|---|---|
|
|
|
|
| 方差守恒型扩散模型 |
|
|
| 方差爆炸型扩散模型 |
1 |
|
| 线性扩散模型 |
|
|
| 广义方差守恒型扩散模型 |
|
|
方差守恒型(Variance-Preserving)扩散模型都遵循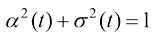 ,这样就可以将扩散过程始终约束在一定范围内。
,这样就可以将扩散过程始终约束在一定范围内。
根据式(1.25),反向计算即可得到方差守恒型扩散模型的漂移系数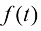 和扩散系数
和扩散系数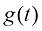 的表达式:
的表达式:
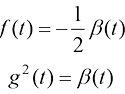 (1.26)
(1.26)
根据扩散过程定义式(1.2),可以得到方差守恒型扩散模型的扩散过程的数学形式:
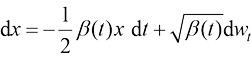 (1.27)
(1.27)
后续章节将详细介绍这几种连续时间扩散模型的建模与训练方法。
离散时间扩散模型
早期的扩散模型也可以离散时间点的形式给出。比如设定T个时间点,然后在每个整数时间点上进行采样和训练,这样的扩散模型称为离散时间扩散模型。
设定数据的分布为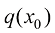 ,扩散模型建模从
,扩散模型建模从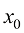 到
到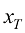 的隐变量的联合分布[即
的隐变量的联合分布[即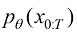 ]作为生成过程,得到扩散过程逆过程的数学形式。假设扩散过程的终态为一个标准高斯分布[即
]作为生成过程,得到扩散过程逆过程的数学形式。假设扩散过程的终态为一个标准高斯分布[即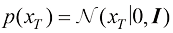 ],则扩散过程的逆过程可以描述为一种概率分布转移:
],则扩散过程的逆过程可以描述为一种概率分布转移:
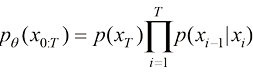 (1.28)
(1.28)
扩散过程逆过程的概率分布转移可以描述和建模为
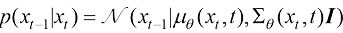 (1.29)
(1.29)
扩散过程的前向过程则定义为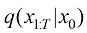 ,它遵循某种设定的规则:
,它遵循某种设定的规则:
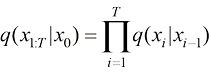 (1.30)
(1.30)
以DDPM(Denoising Diffusion Probabilistic Model,去噪扩散概率模型)[10]为例,其前向过程的概率分布转移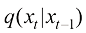 可以使用一组参数
可以使用一组参数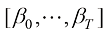 描述为
描述为
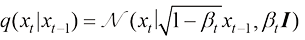 (1.31)
(1.31)
假如标记累乘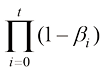 的参数为
的参数为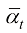 ,则DDPM前向过程的概率分布转移可以描述为
,则DDPM前向过程的概率分布转移可以描述为
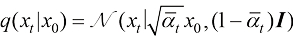 (1.32)
(1.32)
对比式(1.24)和式(1.32),可以看到,DDPM前向过程的概率分布转移与连续时间扩散模型的概率分布转移是等价的,它们都采用高斯分布的形式。
观察表1.1,可以看到,DDPM前向过程的概率分布转移与方差守恒型扩散模型的概率分布转移是等价的:
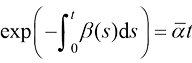 (1.33)
(1.33)
需要注意的是,DDPM的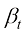 与方差守恒型扩散模型的
与方差守恒型扩散模型的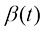 的含义比较相似,但本质不完全相同,它们的物理意义是不同的。比如对于DDPM,当
的含义比较相似,但本质不完全相同,它们的物理意义是不同的。比如对于DDPM,当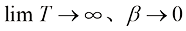 时,根据式(1.32),可得:
时,根据式(1.32),可得:
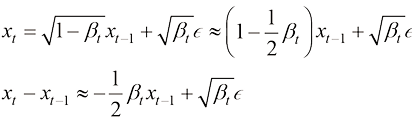 (1.34)
(1.34)
假如将DDPM的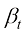 表示为
表示为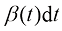 ,根据布朗运动的定义,有
,根据布朗运动的定义,有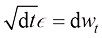 ,于是可以将式(1.34)转换为
,于是可以将式(1.34)转换为
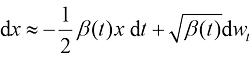 (1.35)
(1.35)
这恰好是方差守恒型扩散模型的扩散过程的数学形式[见式(1.27)]。
根据1.2节对扩散模型的介绍,我们可以利用扩散模型建模一个数据集中数据的分布。但这尚不足以将扩散模型应用于实际问题,因为我们往往希望生成结果的类别或其他属性是可控的。本节讨论赋予扩散模型条件采样能力的两种技术:分类器引导采样和无分类器引导采样。最后讨论用以建模更复杂条件信息的ControlNet。
实际上为了控制生成结果,最简单的做法是以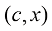 为样本,通过式(1.36)最大化条件似然,得到最终的条件扩散模型。但这么做的一个问题在于需要针对想要采样的每种条件重新训练它们。
为样本,通过式(1.36)最大化条件似然,得到最终的条件扩散模型。但这么做的一个问题在于需要针对想要采样的每种条件重新训练它们。
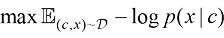 (1.36)
(1.36)
分类器引导采样
分类器引导采样通过利用预先训练好的分类器来控制生成过程。根据贝叶斯公式,可以得到:
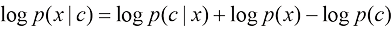 (1.37)
(1.37)
在式(1.37)的两边对x求梯度,你会发现条件得分函数可以表达为
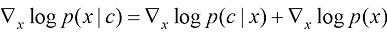 (1.38)
(1.38)
注意与1.2.1小节提到的得分函数不同,这里采用条件得分函数进行采样。式(1.38)可以进一步拓展为
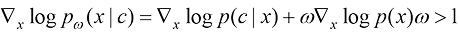 (1.39)
(1.39)
这样就可以通过控制参数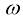 的大小,控制采样结果与条件c的相关性。
的大小,控制采样结果与条件c的相关性。
在实践中,每一步的分类器引导采样可以描述为
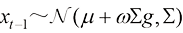 (1.40)
(1.40)
其中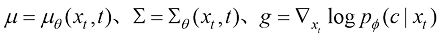 。
。
无分类器引导采样
遗憾的是,分类器引导采样需要的图像分类器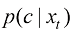 作为一个判别模型会忽略掉
作为一个判别模型会忽略掉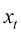 中的大量细节,这种方法无法采样出难以用标签描述的结果(比如想要生成一张包含各种动物的图片)。另外,理想的
中的大量细节,这种方法无法采样出难以用标签描述的结果(比如想要生成一张包含各种动物的图片)。另外,理想的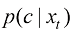 需要能够在任意一个时间步描述
需要能够在任意一个时间步描述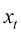 属于每个类别的概率,这对于被噪声破坏过的图片
属于每个类别的概率,这对于被噪声破坏过的图片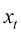 是难以训练的。容易想到的一个极端情况是,对于服从标准高斯分布的
是难以训练的。容易想到的一个极端情况是,对于服从标准高斯分布的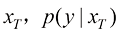 为均匀分布,即
为均匀分布,即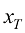 属于每个类别的概率相等。
属于每个类别的概率相等。
一种不需要分类器的技术被提出,名为无分类器引导采样(Classifier-Free Guidance,CFG)。由贝叶斯公式,我们可以得到一个隐式的分类器:
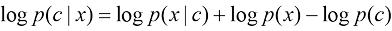 (1.41)
(1.41)
但这要求预先训练两个生成模型,分别为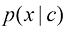 和
和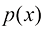 。然而在实践中,我们可以采用共享同一个扩散模型参数的方法来拟合
。然而在实践中,我们可以采用共享同一个扩散模型参数的方法来拟合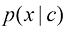 和
和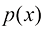 ,要做到这一点,只需要在训练过程中将条件
,要做到这一点,只需要在训练过程中将条件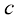 随机置
随机置 即可。训练结束后,我们可以利用这个隐式的分类器得到如下修正后的得分函数:
即可。训练结束后,我们可以利用这个隐式的分类器得到如下修正后的得分函数:
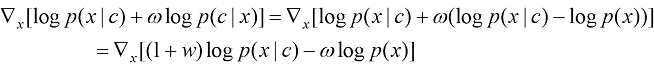
(1.42)
同样,我们也可以通过控制参数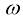 的大小,控制采样结果与条件c的相关性。
的大小,控制采样结果与条件c的相关性。
以T2I生成模型为例,有时候用单纯的文字难以描述我们想要生成的图像。比如我们想要精细地控制所生成人像的姿态,最好能够精细到五指摆放位置或发丝飘动方向的程度。这一点是难以用文字叙述清楚的,并且训练时的文本数据亦难以具备如此精细程度的描述。ControlNet[11]旨在解决这一问题。下面详细介绍ControlNet的原理及背后的思想,最后展示一些ControlNet生成结果。
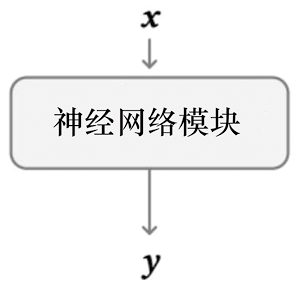
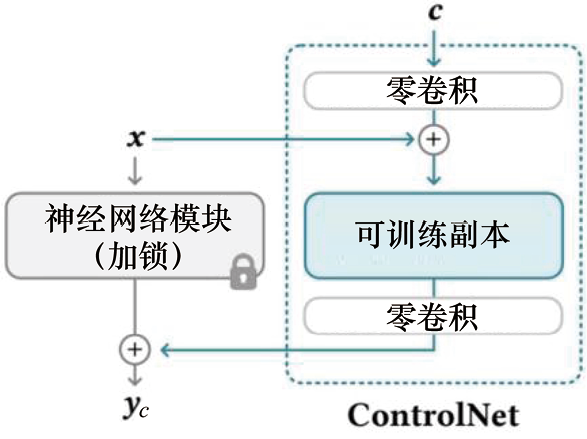
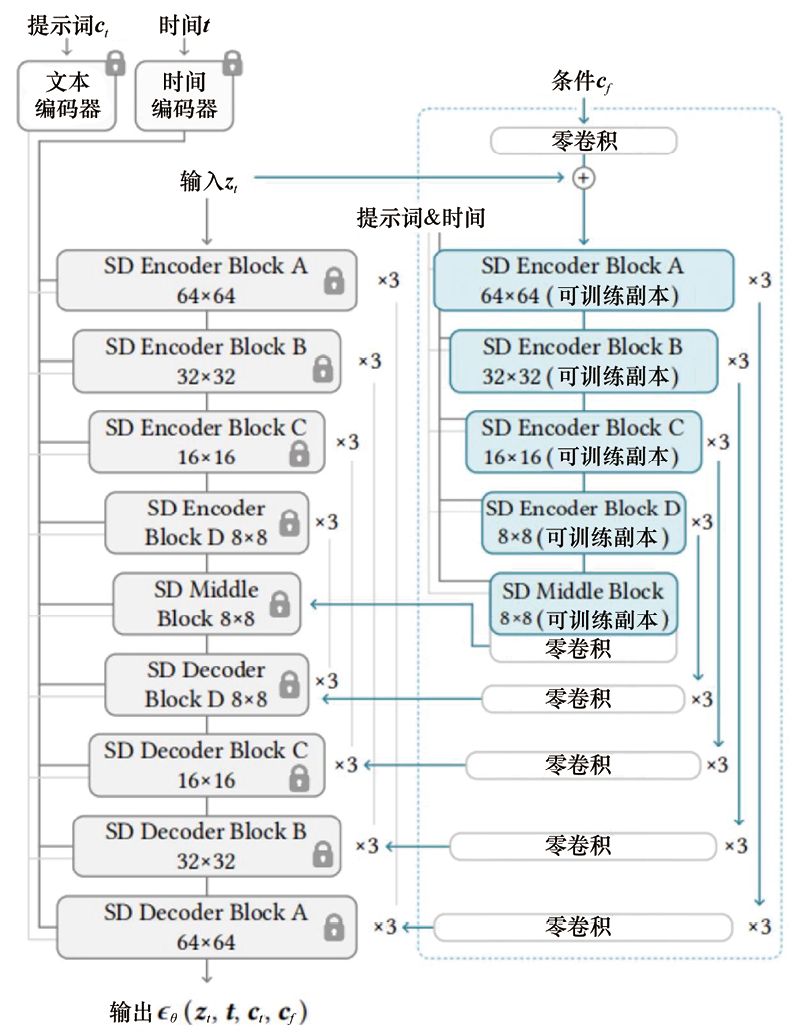
ControlNet是一种通过引入空间定位和特定任务图像条件来增强大型T2I生成模型的神经网络架构。与条件采样方法运用场景不同,在运用ControlNet之前需要先训练扩散模型。ControlNet的核心思想如图1.1所示。ControlNet会向神经网络模块注入额外的条件信息。
(a)应用ControlNet之前
(b)应用ControlNet之后
图1.1 ControlNet的核心思想[11]
在此,我们使用术语神经网络模块指代一组神经网络层,它们通常链接在一起形成一个神经网络单元,如resnet模块、conv-bn-relu模块、multi-head attention模块以及transformer 模块等。如图1.1(a)所示,假设一个训练收敛的神经网络模块可以形式化为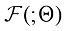 ,网络模块参数为
,网络模块参数为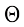 ,则使用
,则使用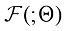 将输入特征图
将输入特征图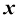 变换为另一个特征图
变换为另一个特征图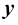 的操作可以形式化为
的操作可以形式化为
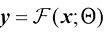 (1.43)
(1.43)
如图1.1(b)所示,ControlNet会复制神经网络模块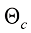 ,并在该神经网络模块输入前和输出后分别连接一个权重(Weight)和偏置(Bias)初始化为0、卷积核大小为1×1的卷积层。在训练过程中,冻结原本的网络模块参数
,并在该神经网络模块输入前和输出后分别连接一个权重(Weight)和偏置(Bias)初始化为0、卷积核大小为1×1的卷积层。在训练过程中,冻结原本的网络模块参数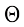 。ControlNet从输入到输出的变换可以形式化为
。ControlNet从输入到输出的变换可以形式化为
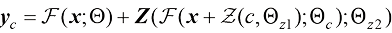 (1.44)
(1.44)
通过这样的设计,在ControlNet训练开始时,有害的噪声不会影响到可训练副本的隐藏层。此外,由于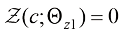 且可训练副本仅接收输入特征图
且可训练副本仅接收输入特征图 ,这个可训练副本具有完整的功能,保留了大型预训练模型的能力,可作为进一步学习的强大骨干。零卷积则通过消除在初始训练步骤中作为梯度的随机噪声来保留主干网络的信息。
,这个可训练副本具有完整的功能,保留了大型预训练模型的能力,可作为进一步学习的强大骨干。零卷积则通过消除在初始训练步骤中作为梯度的随机噪声来保留主干网络的信息。
下面我们具体以SD1.5 U-Net为例来展示ControlNet如何将条件控制添加到一个大型的预训练扩散模型中。稳定扩散本质上是一个带有一个编码器、一个中间块和一个跳过连接解码器的U-Net 。编码器和解码器都包含12个块,完整的模型包含25个块,包括中间块。在这25个块中,8个块是下采样或上采样卷积层,而其他17个块是主块,每个主块包含4个残差网络层和2个视觉Transformer(ViT)。每个ViT都包含几种交叉注意力和自注意力机制。例如,如图1.2(a)所示,“SD Encoder Block A”包含4个ResNet 层和2个ViT,而“ ”表示该块重复了3次。对于文本提示采用CLIP文本编码器,并且扩散时间戳采用一个使用位置编码的时间编码器编码。如图1.2(b)所示,可将ControlNet应用于SD1.5 U-Net的每个编码器级别。ControlNet创建了12个编码块和1个稳定扩散中间块的可训练副本。12个编码块有4个分辨率(64×64、32×32、16×16和8×8),每个编码块重复3次。输出则被添加到SD1.5 U-Net的12个残差连接块和1个中间块中。
”表示该块重复了3次。对于文本提示采用CLIP文本编码器,并且扩散时间戳采用一个使用位置编码的时间编码器编码。如图1.2(b)所示,可将ControlNet应用于SD1.5 U-Net的每个编码器级别。ControlNet创建了12个编码块和1个稳定扩散中间块的可训练副本。12个编码块有4个分辨率(64×64、32×32、16×16和8×8),每个编码块重复3次。输出则被添加到SD1.5 U-Net的12个残差连接块和1个中间块中。
(a)稳定扩散 (b)ControlNet
图1.2 将ControlNet应用于SD1.5 U-Net[11]
一些ControlNet生成结果如图1.3所示。

图1.3 一些ControlNet生成结果[11]
自DDPM问世以来,扩散模型在文生图领域迅速崭露头角,其创新性和应用潜力受到学术界和工业界的广泛关注。然而,生成速度问题一直是扩散模型面临的一大挑战。在DDPM框架下,生成一幅高质量的图像往往需要Denoiser进行数千次的迭代推断,这一过程无疑增加了生成图像的时间成本。
在过去两年中,学术界和工业界围绕如何提升扩散模型采样效率这一核心问题,展开了深入的研究和探索。众多研究者提出了一系列创新的方法和策略,旨在缩短图像生成的时间,提高扩散模型的实用性和效率。本节旨在对这些研究成果进行系统的梳理和总结,以期为读者提供一个清晰的视角来了解当前扩散模型采样加速领域的最新进展和背后的原理。
通过深入分析和评估这些加速方法,我们可以看到,尽管挑战依然存在,但通过不断的技术创新和优化,扩散模型在图像生成速度上已经有了显著的提升。这不仅推动了扩散模型在实际应用中的广泛部署,也为扩散模型未来的研究和开发提供了宝贵的经验和启示。
扩散模型的应用可以分为两个相互解耦的阶段:训练和推断。根据加速方法是否需要改变扩散模型的标准训练过程(如DDPM的标准训练过程),这些加速方法可以分为两类:training-free加速采样方法和training-based加速采样方法。
training-free加速采样方法独立于扩散模型的训练过程,即仅改变标准扩散模型的推断采样过程。本节首先介绍DPM-Solver[12],它通过将推断过程由随机微分方程(Stochastic Differential Equation,SDE)转换为常微分方程(Ordinary Differential Equation,ODE),并通过平衡ODE求解精度和采样速度,实现采样过程的加速。你会发现,扩散模型采样加速的开山之作DDIM[13]就是一阶DPM-Solver。
下面首先介绍扩散模型的采样过程可以用什么样的SDE和ODE来描述,然后介绍DPM-Solver是如何近似求解采样过程ODE的,最后展示DPM-Solver的加速采样效果。
让我们从连续时间扩散模型出发,每一时刻下带噪声的图像的分布可以用一个高斯分布来刻画:
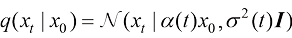 (1.45)
(1.45)
根据Song等人的工作,连续时间扩散模型的扩散过程和逆过程可以分别用如下两个SDE来刻画:
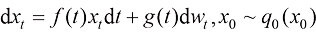 (1.46)
(1.46)
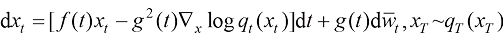 (1.47)
(1.47)
其中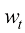 和
和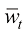 是两个相互独立的标准维纳过程,且函数
是两个相互独立的标准维纳过程,且函数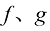 和变量
和变量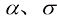 之间存在如下关系:
之间存在如下关系:
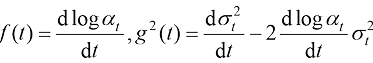 (1.48)
(1.48)
此外,DDPM中的去噪函数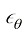 实际上拟合的就是
实际上拟合的就是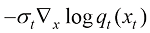 ,因此连续时间扩散模型的采样过程(逆过程)SDE也可以表达为
,因此连续时间扩散模型的采样过程(逆过程)SDE也可以表达为
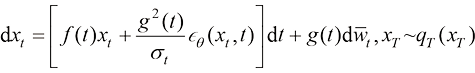 (1.49)
(1.49)
DDPM的标准采样过程则可以看作式(1.49)的一阶SDE求解器。
事实上,Song等人证明了式(1.47)所表达的SDE与式(1.50)所表达的概率流ODE是对应的,两种过程中每一时刻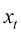 下的边缘分布
下的边缘分布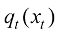 完全相等:
完全相等:
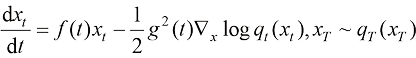 (1.50)
(1.50)
同样,用去噪函数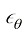 替换
替换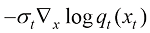 ,可以得到如下ODE:
,可以得到如下ODE:
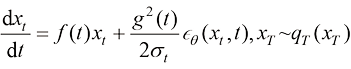 (1.51)
(1.51)
式(1.47) 所表达的SDE和式(1.50)所表达的概率流ODE都能采样出真正的图像分布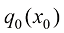 ,但相比求解SDE,求解ODE更容易。DPM-Solver的核心工作便是利用现成的数学工具快速求解ODE。
,但相比求解SDE,求解ODE更容易。DPM-Solver的核心工作便是利用现成的数学工具快速求解ODE。
事实上,式(1.50)所表达的概率流ODE又称半线性ODE,这是因为式(1.50)右边的前一半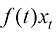 与
与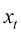 成线性关系,而后一半包含
成线性关系,而后一半包含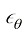 所表达的非线性函数。利用现成的求解半线性ODE的技巧——常数变易法,可以精确计算出式(1.50)所表达的概率流ODE 的解,其中
所表达的非线性函数。利用现成的求解半线性ODE的技巧——常数变易法,可以精确计算出式(1.50)所表达的概率流ODE 的解,其中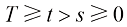 :
:
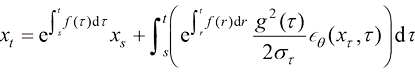 (1.52)
(1.52)
通过换元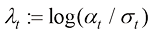 并代入式(1.48),可以将式(1.52)化简为
并代入式(1.48),可以将式(1.52)化简为
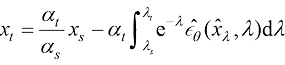 (1.53)
(1.53)
其中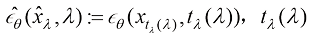 表示
表示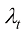 的下标时刻t(因为
的下标时刻t(因为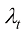 是单调递减函数,所以每个可能的
是单调递减函数,所以每个可能的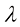 都有唯一对应的t)。
都有唯一对应的t)。
根据式(1.53),对于给定的某个时刻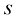 下的去噪结果
下的去噪结果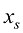 ,如果能对
,如果能对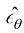 积分,便能精确计算出
积分,便能精确计算出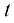 时刻下的去噪结果
时刻下的去噪结果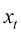 。可惜无法对
。可惜无法对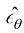 积分,因此只能近似估计式(1.53)右边的后一半。
积分,因此只能近似估计式(1.53)右边的后一半。
假设从连续去噪时间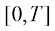 中选取
中选取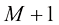 个时间戳,表示为
个时间戳,表示为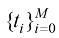 ,其中
,其中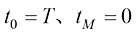 ;则给定
;则给定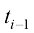 的去噪结果
的去噪结果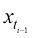 ,根据式
,根据式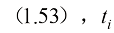 时刻下的去噪结果可以表达为
时刻下的去噪结果可以表达为
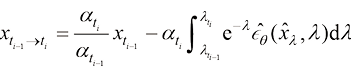 (1.54)
(1.54)
对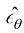 进行k阶泰勒展开,可以得到如下近似结果:
进行k阶泰勒展开,可以得到如下近似结果:
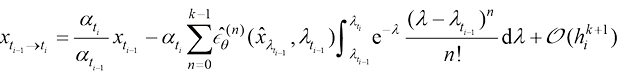
(1.55)
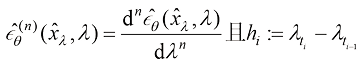 。
。
 Cheng等人证明了通过应用n次分部积分法,式(1.55)中的
Cheng等人证明了通过应用n次分部积分法,式(1.55)中的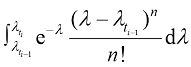 可以解析并计算出来,问题的关键在于如何计算
可以解析并计算出来,问题的关键在于如何计算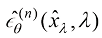 。已经有人研究过这个问题,他们通过利用刚性阶条件(Stiff Order Condition),得到了
。已经有人研究过这个问题,他们通过利用刚性阶条件(Stiff Order Condition),得到了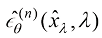 的近似结果。
的近似结果。
关于如何近似计算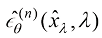 ,见参考文献[14]。
,见参考文献[14]。
在这里,给定任意时刻s下的去噪结果,便可以依据式(1.55)近似求解出s之后任一时刻t的去噪结果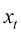 。当然,s与t的时间间隔越大,式(1.55)所示的泰勒展开阶数越低,计算出的
。当然,s与t的时间间隔越大,式(1.55)所示的泰勒展开阶数越低,计算出的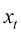 就越不精确。
就越不精确。
DDIM:一阶DPM-Solver
在式(1.55)中,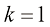 时可以得到一阶DPM-Solver。将
时可以得到一阶DPM-Solver。将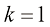 代入式(1.55)可以得到采样公式:
代入式(1.55)可以得到采样公式:
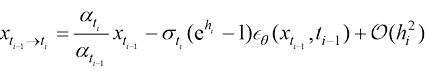 (1.56)
(1.56)
忽略误差项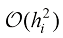 后,可以发现式(1.56)等价于DDIM的采样公式,因此DDIM是一阶DPM-Solver。
后,可以发现式(1.56)等价于DDIM的采样公式,因此DDIM是一阶DPM-Solver。
二阶和三阶DPM-Solver的采样伪代码如图1.4所示[12]。

图1.4 二阶和三阶DPM-Solver的采样伪代码[12]
图1.5展示了DPM-Solver的性能,横轴NFE表示迭代采样时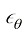 的推断次数,可在固定NFE的前提下比较DPM-Solver和其他采样算法的性能。
的推断次数,可在固定NFE的前提下比较DPM-Solver和其他采样算法的性能。
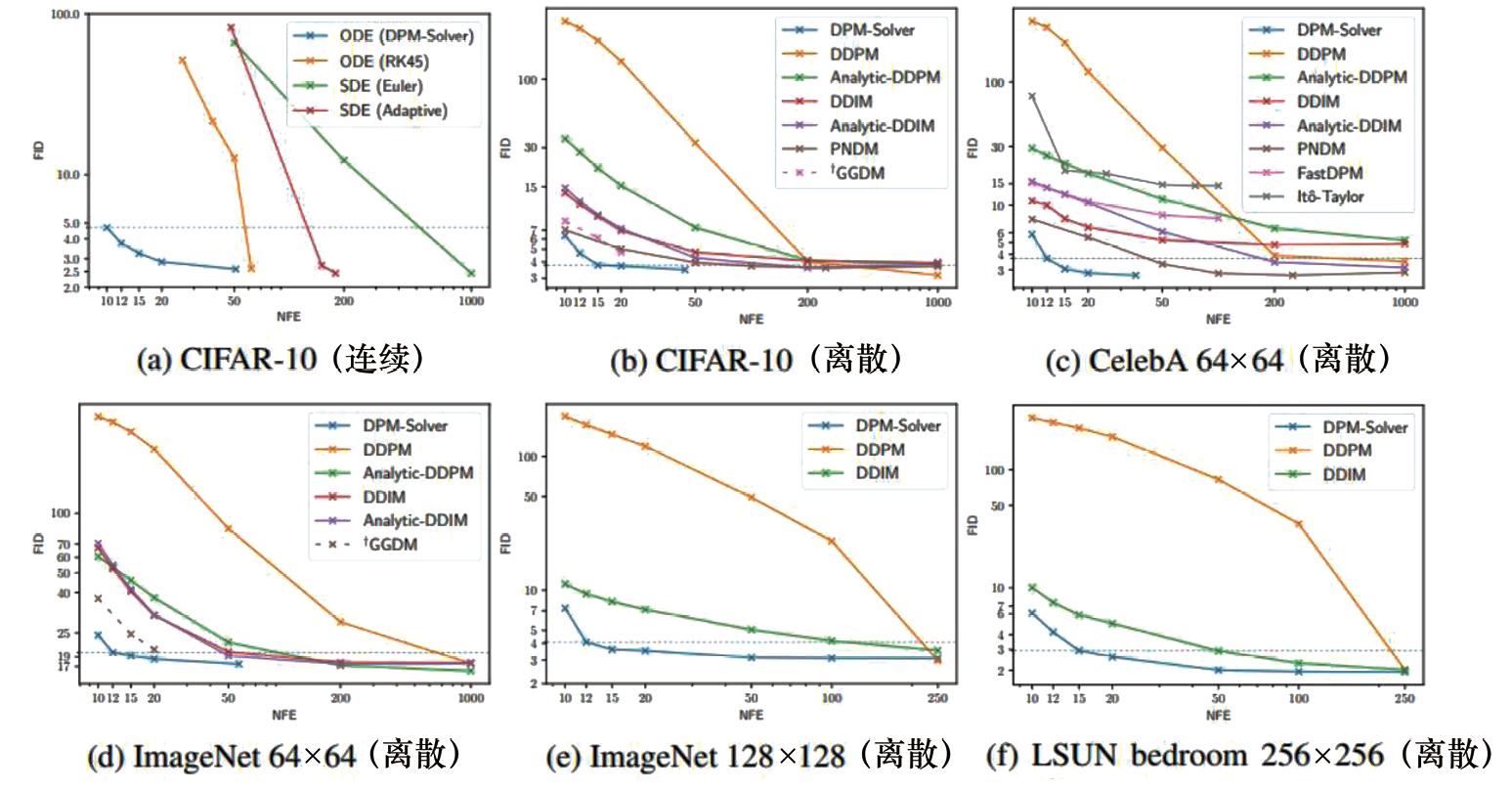
图1.5 DPM-Solver与其他采样算法的性能比较,对于固定的NFE,
DPM-Solver的FID低于其他采用算法[12]
观察DPM-Solver-2和DPM-Solver-3算法的伪代码,不难发现这两种算法在采样下一个时间戳的结果时,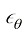 分别需要推断2次和3次,而DPM-Solver-1算法只需要推断一次。DPM-Solver的作者做了以下实验。
分别需要推断2次和3次,而DPM-Solver-1算法只需要推断一次。DPM-Solver的作者做了以下实验。
● 假设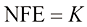 ,对于前
,对于前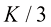 次采样,采用DPM-Solver-3算法迭代去噪;对于最后一次采样,则根据剩余NFE约束采用DPM-Solver-1或DPM-Solver-2算法迭代去噪。
次采样,采用DPM-Solver-3算法迭代去噪;对于最后一次采样,则根据剩余NFE约束采用DPM-Solver-1或DPM-Solver-2算法迭代去噪。
● 对于时间戳的选择,将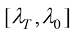 均匀划分为
均匀划分为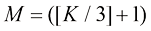 等份,即
等份,即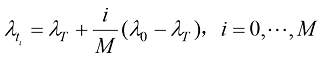 。每个时间步
。每个时间步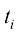 对应于
对应于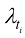 。
。
实验表明,这种时间戳的选择相比均匀划分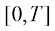 可以带来较大的性能提升。
可以带来较大的性能提升。
均匀划分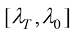 相比直接均匀划分
相比直接均匀划分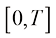 可以带来较大的性能提升。观察
可以带来较大的性能提升。观察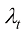 的定义
的定义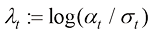 ,不难发现它就是信噪比对数的二分之一。因此这种划分方式会导致在
,不难发现它就是信噪比对数的二分之一。因此这种划分方式会导致在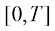 区间上,时间戳更密集地靠近0和T的位置。而早在DPM-Solver被提出以前,Google的研究员便讨论过什么才是DDPM的最优分割方式[15]。通过阅读接下来的内容,读者可以了解到为什么均匀划分
区间上,时间戳更密集地靠近0和T的位置。而早在DPM-Solver被提出以前,Google的研究员便讨论过什么才是DDPM的最优分割方式[15]。通过阅读接下来的内容,读者可以了解到为什么均匀划分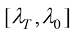 相比直接均匀划分
相比直接均匀划分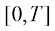 可以带来较大的性能提升。
可以带来较大的性能提升。
扩散模型的训练和推断过程是解耦的,假设训练阶段的扩散过程由T个时间戳分割: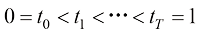 ,采样时可以选择其中的一个子集
,采样时可以选择其中的一个子集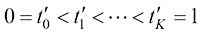 作为
作为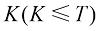 个采样时间戳。事实上,可以通过估算以这一套采样时间戳采样得到的x0分布的ELBO(Evidance Lower BOund,证据下界)来评价这套采样时间戳设计的好坏。根据ELBO的分解性,这套采样时间戳
个采样时间戳。事实上,可以通过估算以这一套采样时间戳采样得到的x0分布的ELBO(Evidance Lower BOund,证据下界)来评价这套采样时间戳设计的好坏。根据ELBO的分解性,这套采样时间戳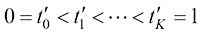 的优劣可以用以下损失函数来量化:
的优劣可以用以下损失函数来量化:
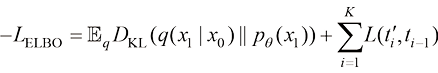 (1.57)
(1.57)
其中:
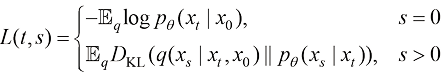 (1.58)
(1.58)
观察式(1.57)和式(1.58)可以发现,寻找最优采样时间戳方案其实可以转换为求解最短路径问题。每两个时间戳t和s之间的距离便由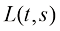 给出。实际上, 可以采用蒙特卡洛采样来估计每一个可能的
给出。实际上, 可以采用蒙特卡洛采样来估计每一个可能的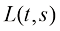 ,因此在近似得到每个
,因此在近似得到每个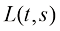 之后,可以采用Dijkstra算法求得最短路径并确定最优采样时间戳方案。
之后,可以采用Dijkstra算法求得最短路径并确定最优采样时间戳方案。
在参考文献[12]中,DPM-Solver的作者通过实验对每个固定的K值,展示了最优采样时间戳方案的可视化结果,如图1.6所示。
图1.6的左图展示了基于DDPM损失函数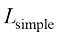 在CIFAR10数据集上训练完成的最优采样时间戳方案的可视化结果。横轴表示训练时间戳从1到1 000,纵轴表示K值。采样时间戳主要集中在接近
在CIFAR10数据集上训练完成的最优采样时间戳方案的可视化结果。横轴表示训练时间戳从1到1 000,纵轴表示K值。采样时间戳主要集中在接近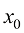 的区域。图1.6的右图则展示了基于参考文献[16]提出的损失函数
的区域。图1.6的右图则展示了基于参考文献[16]提出的损失函数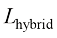 在ImageNet 64×64数据集上训练完成的最优采样时间戳方案的可视化结果。可以看到,采样时间戳主要集中在接近0和T的区域。这一现象与DPM-Solver实验中的结果相吻合。
在ImageNet 64×64数据集上训练完成的最优采样时间戳方案的可视化结果。可以看到,采样时间戳主要集中在接近0和T的区域。这一现象与DPM-Solver实验中的结果相吻合。
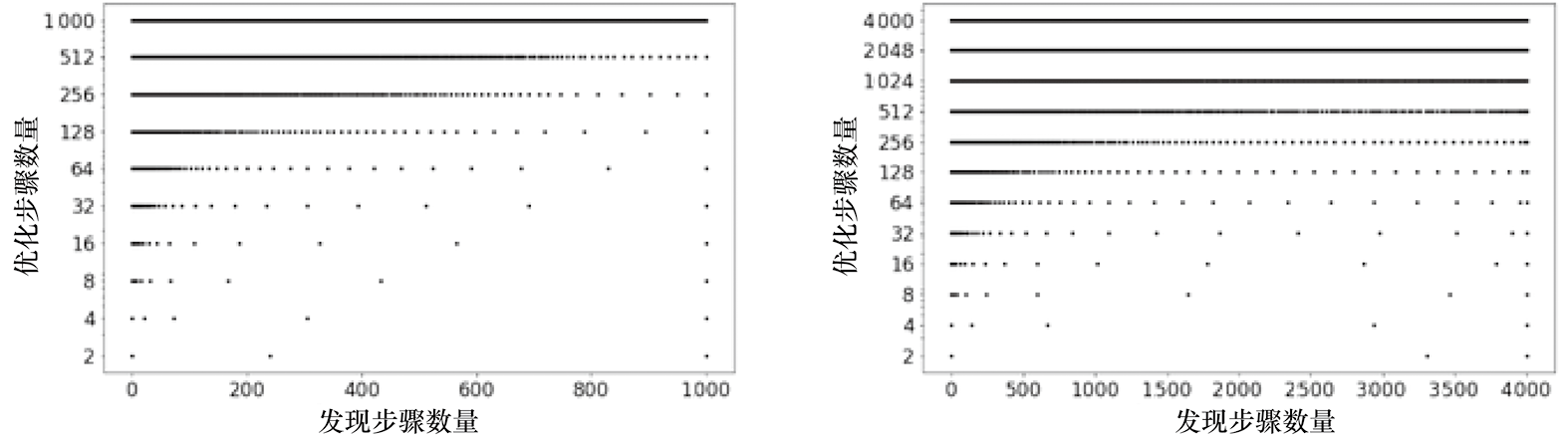
图1.6 最优采样时间戳方案的可视化结果[15]
接近0的采样步骤很重要,因为这些采样步骤可以捕捉到更精细的图像细节。此外,算法会额外分配一些采样时间戳在靠近T的位置,这可能是为了在采样早期更好地突破分布模态,采样到一些低概率的模态,从而带来更多的ELBO收益。
本小节从两个角度介绍了training-free加速采样方法。DPM-Solver旨在利用ODE建模扩散模型的采样过程,并通过近似求解ODE来获得最终采样结果,经典的加速采样算法DDIM就是一阶DPM-Solver。在DPM-Solver算法执行过程中,两个时间戳距离越近(采样轮次越多),DPM-Solver阶数越高(Denoiser推断次数越多),对下一步的采样结果估计越准确,但速度越慢。部分参考文献还补充了对采样时间戳选择方面的考虑。笔者猜测结合部分参考文献中的最优采样时间戳方案,DPM-Solver的性能或许可以得到进一步提升。
与training-free加速采样方法不同,training-based加速采样方法往往修改了扩散模型的训练阶段。本小节将介绍近年来出现的比较有效的training-based加速采样方法。
这种加速采样方法出自参考文献[17],它的出发点很简单:另外两类生成模型VAE和GAN虽然不能像扩散模型一样精细地建模高维数据分布,但它们的采样仅需要推断一次Decoder或Generator。或许可以利用这一点来加速扩散模型采样。原作者将这种加速采样方法命名为Early-Stopped DDPM(简称ES-DDPM),ES-DDPM原理示意如图1.7所示。

图1.7 ES-DDPM原理示意[17]
ES-DDPM截断了扩散模型的训练,生成过程和采样过程仅考虑区间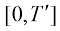 ,使得原本的扩散模型训练损失函数变为
,使得原本的扩散模型训练损失函数变为
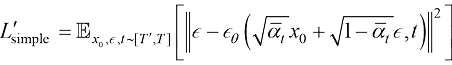 (1.59)
(1.59)
但采样时会出现问题,因为不知道初始分布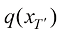 是什么。ES-DDPM考虑在原本的图像数据集上训练一个VAE,这样就可以用
是什么。ES-DDPM考虑在原本的图像数据集上训练一个VAE,这样就可以用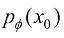 粗略地建模原始数据集分布
粗略地建模原始数据集分布 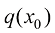 。其中VAE损失函数如下:
。其中VAE损失函数如下:
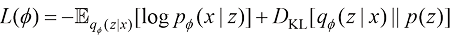 (1.60)
(1.60)
之后通过对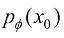 的采样结果执行扩散过程,就可以得到分布
的采样结果执行扩散过程,就可以得到分布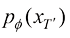 以近似分布
以近似分布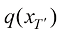 。这样采样时便可以将原本扩散模型从T到T'的采样过程合并为对VAE Decoder的一次推断,从而达到加速效果。
。这样采样时便可以将原本扩散模型从T到T'的采样过程合并为对VAE Decoder的一次推断,从而达到加速效果。
这种加速采样方法出自参考文献[18],旨在针对预训练的扩散模型进行多阶段蒸馏,以使最终蒸馏后的模型能够基于更少的采样步数采样出与原始扩散模型相似的输出分布。原作者将这种加速采样方法命名为“Progressive Distillation”。
Progressive Distillation原理示意如图1.8所示,蒸馏前的模型记作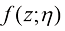 ,它只需要4个采样步即可从初始噪声中采样出
,它只需要4个采样步即可从初始噪声中采样出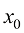 。在每一阶段蒸馏过程中,会将相邻的两个采样步合并为一个采样步,这样两阶段蒸馏后的模型
。在每一阶段蒸馏过程中,会将相邻的两个采样步合并为一个采样步,这样两阶段蒸馏后的模型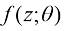 便仅需要一个采样步。
便仅需要一个采样步。
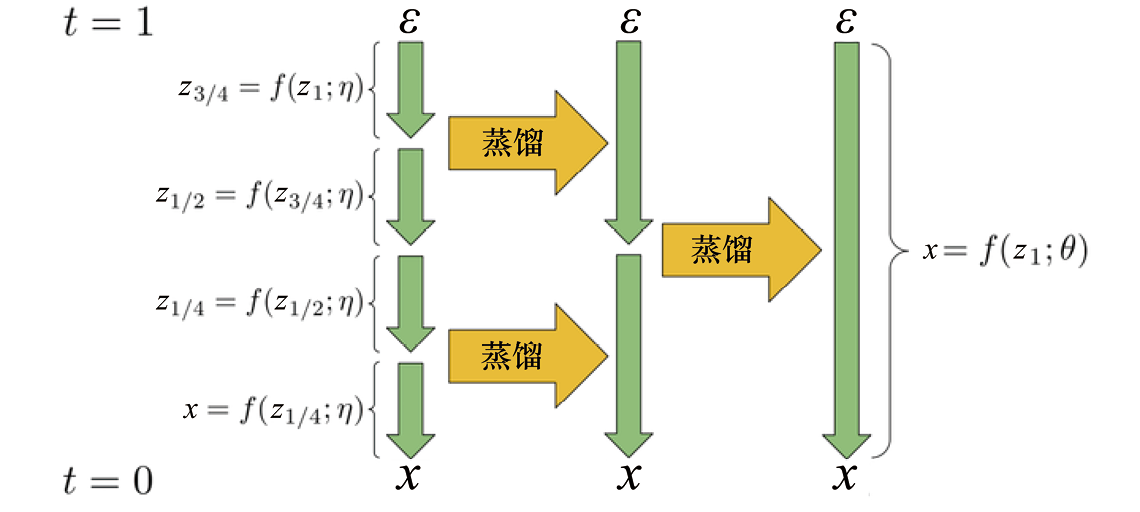
图1.8 “Progressive Distillation”原理示意,此处展示了多阶段蒸馏的过程[18]
标准扩散模型训练伪代码和“Progressive Distillation”训练伪代码如图1.9所示,相比标准扩散模型训练过程,“Progressive Distillation”额外增加了绿色部分的内容。从伪代码中可以看出,模型会经过K个阶段的蒸馏,每一阶段结束后,就会得到采样步数为原先一半的采样器,并作为下一轮蒸馏的“教师模型”。在每一阶段蒸馏过程中,可利用DDIM采样得到“教师模型”两步去噪后的目标,然后训练“学生模型”去预测这一目标,直至“学生模型”收敛。
实际上,与DPM-Solver相比,“Progressive Distillation”稍显过时。因为根据前面对DPM-Solver的介绍,DDIM本身采样质量(ODE求解精度)要弱于高阶DPM-Solver,并且基于DDIM训练“Progressive Distillation”得到的蒸馏模型会丢失预训练扩散模型的许多信息(比如无法像预训练扩散模型一样预测每一步的噪声或分数)。此外,相比training-free加速采样方法,“Progressive Distillation”需要额外的训练开销。不过这种多阶段蒸馏的方法是值得关注的,或许在其他场景下可以考虑采用这种蒸馏方法。

图1.9 标准扩散模型训练伪代码和“Progressive Distillation”训练伪代码[18]
除了上述提到的加速采样方法,training-based加速采样方法还有很多。比如参考文献[19]利用傅里叶积分算子构建时态卷积块,训练后的模型能够直接输出整个采样轨迹。再比如,参考文献[20]通过学习沿着直线路径传输分布的ODE模型(与DDPM不同,这是一种新的分布变换过程),并利用并行解码和优化的路径选择来显著加快采样过程。
[1] HINTON G E. Deep belief networks[J]. Scholarpedia, 2009, 4(5): 5947.
[2] KINGMA D P, WELLING M. Auto-Encoding Variational Bayes[EB/OL]. arXiv: 1312.6114.
[3] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Communications of the ACM, 2020, 63(11): 139-144.
[4] VAN DEN OORD A, KALCHBRENNER N, VINYALS O, et al. Conditional image generation with PixelCNN decoders[C] //Advances in Neural Information Processing Systems, 2016.
[5] FINLAY C, JACOBSEN J H, NURBEKYAN L, et al. How to train your neural ODE: The world of Jacobian and kinetic regularization[C]//International Conference on Machine Learning. 2020: 3154-3164.
[6] VINCENT P. A connection between score matching and denoising autoencoders[J]. Neural Computation, 2011, 23(7): 1661-1674.
[7] LIPMAN Y, CHEN R T Q, BEN-HAMU H, et al. Flow matching for generative modeling[EB/OL]. arXiv: 2210.02747.
[8] TONG A, FATRAS K, MALKIN N, et al. Improving and generalizing flow-based generative models with minibatch optimal transport[EB/OL]. arXiv: 2302.00482.
[9] KARRAS T, AITTALA M, AILA T, et al. Elucidating the design space of diffusion-based generative models[C]// Advances in Neural Information Processing Systems. 2022, 35: 26565-26577.
[10] HO J, JAIN A, ABBEEL P. Denoising diffusion probabilistic models[C]//Advances in Neural Information Processing Systems. 2020, 33: 6840-6851.
[11] ZHANG L, RAO A, AGRAWALA M. Adding conditional control to text-to-image diffusion models[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2023: 3836-3847.
[12] LU C, ZHOU Y, BAO F, et al. DPM-Solver: A fast ODE solver for diffusion probabilistic model sampling in around 10 steps[C]//Advances in Neural Information Processing Systems. 2022, 35: 5775-5787.
[13] SONG J, MENG C, ERMON S. Denoising diffusion implicit models[EB/OL]. arXiv: 2010.02502.
[14] HOCHBRUCK M, OSTERMANN A. Explicit exponential runge-kutta methods for semilinear parabolic problems[J]. SIAM Journal on Numerical Analysis, 2005, 41(2): 786-803.
[15] WATSON D, HO J, NOROUZI M, et al. Learning to efficiently sample from diffusion probabilistic models[EB/OL]. arXiv: 2106.03802.
[16] NICHOL A, DHARIWAL P. Improved denoising diffusion probabilistic models[EB/OL]. arXiv: 2102.09672.
[17] LYU Z, XU X, YANG C, et al. Accelerating diffusion models via early stop of the diffusion process[EB/OL]. arXiv: 2205.12524.
[18] SALIMANS T, HO J. Progressive distillation for fast sampling of diffusion models[EB/OL]. arXiv: 2202.00512.
[19] ZHENG H, NIE W, VAHDAT A, et al.Fast sampling of diffusion models via operator learning[EB/OL]. arXiv: 2211.13449.
[20] LIU X, GONG C, LIU Q. Flow straight and fast: Learning to generate and transfer data with rectified flow[EB/OL]. arXiv: 2209.03003.