

书名:流体状态方程与热物性参数计算
ISBN:978-7-115-64395-7
本书由人民邮电出版社发行数字版。版权所有,侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用,未经授权,不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟,与我们共同保护知识产权。
如果购买者有侵权行为,我们可能对该用户实施包括但不限于关闭该帐号等维权措施,并可能追究法律责任。
著 苑伟民
责任编辑 李永涛
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
网址 http://www.ptpress.com.cn
读者服务热线:(010)81055410
反盗版热线:(010)81055315
本书以流体状态方程及流体热物性参数计算为主线,分为流体状态方程,量纲及伪量纲分析,偏导数和微积分及热力学关系式,状态方程中 p、V、T、Z 之间的导数,剩余性质与偏离函数,流体的热物性参数计算,MATLAB 编程基础知识,实时编辑器与MATLAB编程求解流体热物性参数实例 9 章内容。本书在讲解流体状态方程和流体热物性参数计算过程中,将公式分步推导,并辅以大量计算实例,便于读者理解和使用公式。
本书适合油气储运工程、石油炼制工程、燃气输配工程、通风与空调工程、化学工程等相关专业的学生学习,也可供从事天然气、二氧化碳气体、氢气、掺氢天然气等气态、液态石油化工产品的加工、输送、存储、管理、设计工作的人员及相关专业技术人员参考。
在我国多元化的能源结构中,天然气作为一种优质、高效的清洁能源,将成为主体能源。天然气管道工程建设和液化天然气站工程建设是天然气产业链中的两个主要板块。工程实践证明,先进和可靠的技术必须依赖于准确、完善和科学的基础知识。
本书是编者多年来努力学习、虚心讨教、潜心研究的结果,是对天然气等流体热物性参数及其编程计算领域做出的一大贡献。
本书内容丰富,公式推导严谨,对流体的热物性参数进行了深入浅出的推导、验证和编程计算;以天然气热物性参数求解为背景,将数值算法与计算机编程相结合,列举了综合应用实例;对国内外的相关研究成果进行了介绍。
本书可用作相关专业的教学书和参考书。
本书编写主要围绕3个方面:一是完善流体状态方程和热物性参数计算公式的推导过程,对常用流体热物性参数的计算公式进行分步推导,并对不同形式的公式进行对比分析,弥补目前大多数图书中只有公式而没有推导过程的缺憾;二是抛砖引玉,在对流体状态方程和热物性参数研究的基础上,提出新的研究方法和新的计算公式,引导读者扩展研究思路;三是介绍计算机编程软件在科学研究中的应用,采用计算机辅助计算来加速读者对专业知识研究的进程。
本书分为2篇,共9章。第1篇分为6章内容,主要介绍流体状态方程及流体热物性参数的计算。第1章深入浅出地介绍流体状态方程的发展历程,让读者了解流体状态方程发展的阶段,如给出Starling早期提出的两个BWRS状态方程(这两个状态方程在其他文献中很少有介绍),引导读者对状态方程做进一步的研究,并对常用的 RK、SRK、PR、BWRS、LKP 状态方程进行对比态转化,使读者能够使用各种形式的状态方程进行计算。第 2 章利用量纲分析的成果,提出伪量纲分析的概念,并对5个常用的状态方程进行伪量纲分析,给出流体热物性参数的4 类单位组合,同时指出利用伪量纲分析的成果,既可以不用在计算过程中和计算后进行单位制转化就得到相应单位的热物性参数,又可以将5个常用的状态方程中体积形式的密度转化为质量形式的密度,如直接使用密度单位为 kg/m3形式的状态方程进行密度求解,求解出的密度是以kg/m3为单位的。第 3 章将偏导数和微积分等数学知识与热力学关系式相结合,介绍一阶偏导数和二阶偏导数的求导和应用,分别以T和V、T和p、p和V为独立变量进行熵、焓关系式的推导;在不定积分和定积分的介绍中,以RK状态方程为例推导RK状态方程的偏导数。第4章对5 个常用状态方程中的 p、V、T、Z 之间的导数进行一一推导,给出推导过程和结果,便于读者研究和使用。第 5 章分别对剩余性质和偏离函数进行介绍,对剩余性质的熵、焓与 p、V、T 的关系式,偏离函数关系式,比热容,比热容比(绝热指数),微分等熵膨胀效应系数,等温压缩率系数,等熵压缩率系数,等压体积膨胀系数,焦耳-汤姆孙系数的计算公式进行推导,并以 RK 状态方程为例进行偏离函数的推导,为第 6 章中真实流体的热物性参数计算奠定理论基础。第6章首先介绍理想气体焓、熵、比热容的计算公式,然后分别采用5个常用的状态方程对实际流体的压缩因子、(比)焓、(比)熵、比热容、焦耳-汤姆孙系数、黏度等热物性参数求解的方程进行一一推导并给出计算实例;对以往图书中鲜有出现的部分参数,如立方型状态方程中一阶和二阶温度导数的推导进行讲解,给出多种推导的方法和多个推导出的公式,使读者在学习专业知识的同时,不但知其然,而且知其所以然;此外,在 6.8 节中对行业内主流的流体计算软件Aspen HYSYS、PipelineStudio,以及权威性较高的图书API Technical Data Book中理想气体比热容、焓、熵的计算公式分别进行介绍,同时对国际标准Natural gas — Calculation of thermodynamic properties — Part 1: Gas phase properties for transmission and distribution applications(ISO 20765-1:2005)中理想气体比热容、焓、熵的计算公式进行介绍,并根据该标准中比热容的计算公式,经过严格的数学推导,分别提出 3 个新的理想气体焓、熵计算公式,以帮助读者加深对比热容、焓、熵计算公式的理解。第 2 篇分为 3 章内容,主要介绍计算机辅助编程,选取MATLAB进行讲解。第7章对MATLAB编程中用到的格式输出函数、人机交互对话、Excel表格读取、多项式求根、非线性方程求解等主要函数进行介绍;第8章详细介绍MATLAB中的实时编辑器,包括实时脚本的建立、编写代码、运行代码、调试代码、插入控件、格式化文件、发布代码等内容;第9章采用M文件和实时编辑器分别对MBWRSY状态方程和PR状态方程进行实例编程,并对代码进行解释,使读者能够快速掌握编程的技巧,解决类似辅助计算的编程问题,避免走“编程要学习大量算法”的弯路,尽量让读者把时间花在对专业知识的学习上,而非计算机编程上。
本书从开始至成稿经历了十几年的打磨。在这十几年中,西南石油大学贺三教授、贾文龙教授,上海交通大学顾安忠教授,中国石油大学(华东)李玉星教授、唐建峰教授,中国石油大学(北京)宫敬教授、李兆慈教授,西安石油大学王寿喜教授,中国石油规划设计总院原院长苗承武高级工程师,白改玲教授级高级工程师,上海石油天然气有限公司原总工程师郭揆常教授级高级工程师,安徽省充换电有限责任公司曹根苗副总经理等,曾在本书编写的不同阶段给予指导和帮助,在此一并致以崇高的谢意。
由于编者水平有限,书中难免存在不妥之处,欢迎广大读者对书中内容提出宝贵意见和建议,以便进行修改,编者邮箱:yuanvmin@hotmail.com。
苑伟民
2025年1月
本篇分为6章内容,主要介绍流体状态方程和流体热物性参数及其公式的推导。第1章介绍流体状态方程的发展历程,并对常用的RK、SRK、PR、BWRS、LKP状态方程进行对比态转化。第2章利用量纲分析的成果,提出伪量纲分析的概念,并对5个常用的状态方程进行伪量纲分析。第3章将偏导数和微积分等数学知识与热力学关系式相结合,分别以T和V、T和p、p和V为独立变量进行熵、焓关系式的推导。第4章对常用的5个状态方程中的p、V、T、Z之间的导数一一进行分步推导,便于读者研究和使用。第5章分别对剩余性质和偏离函数进行介绍。第6章首先介绍理想气体焓、熵、比热容的公式,然后分别使用5个常用的状态方程对实际流体的压缩因子、(比)焓、(比)熵、比热容、焦耳-汤姆孙系数、黏度等热物性参数求解的方程进行分步推导并给出计算实例;对诸如立方型状态方程中一阶和二阶温度导数等鲜有图书介绍的推导过程进行讲解;此外,在 6.8 节中对主流软件Aspen HYSYS、PipelineStudio,以及API Technical Data Book一书中理想气体的比热容、焓、熵公式进行介绍。
状态方程就是在状态参数之间建立的函数关系,比如,由两个状态参数来计算其他状态参数的函数关系。状态参数有很多,我们所讨论的流体动力学范围内有压力、温度和密度,它们都会出现在运动方程中。
计算密度、压缩因子、焓、熵、比热容、比热容比、焦耳-汤姆孙系数等天然气的热物性参数,需要用到状态方程。本章在介绍流体状态方程发展的同时,对雷德利希-邝方程(Redlich-Kwong Equation,简称RK状态方程、RK方程)、索阿韦-雷德利希-邝方程(Soave-Redlich-Kwong Equation,简称SRK状态方程、SRK方程)、彭-罗宾森方程(Peng-Robinson Equation,简称PR状态方程、PR方程)、本尼迪克特-韦布-鲁宾-斯塔林方程(Benedict-Webb-Rubin-Starling Equation,简称BWRS状态方程、BWRS方程)、李-凯斯勒-普洛克方程(Lee-Kesler-Plocker Equation,简称LKP状态方程、LKP方程)等进行研究、讨论。
包含理想气体状态方程在内的状态方程,在各种文献中不下 150 种,有的是根据理论分析得到的,有的是由实验数据拟合的,有的是用理论分析和实验数据相结合而推导出的;但只有少数方程通用性比较好,并没有哪一种状态方程能够独占鳌头。对状态方程的研究一直都在进行,新方程仍在不断涌现。
状态方程既简单又精确的分类方法是按照其起源分类。按照这一方法,将状态方程分为范德华族立方方程(立方型状态方程)、扩展的维里族方程(维里型状态方程)、对比态方程以及基于晶格模型的统计热力学模型、扰动模型和积分方程,或者基于计算机拟合数据得到的方程。本书主要对前两种方程进行研究,这两种方程的主要发展路线可总结为:(1)立方型状态方程——van der Waals(vdW)(1873 年)→Redlich-Kwong(RK)(1949 年)→Wilson(1964 年)→Soave(SRK)(1972年)→Peng-Robinson(PR)(1976年)→Patel-Teja(PT)(1982年);(2)维里型状态方程——Thiesen(1885年)→Kamerlingh Onnes(1901年)→Beattie-Bridgeman(BB)(1928年)→Benedict-Webb-Rubin(BWR或者称为MBB)(1940年)→Starling(BWRS)(1971年)→Starling-Han(BWRSH)(1972年)→Starling等人(AGA天然气方程)(1991年)。
理想气体状态方程(Ideal Gas Equation of State),又称理想气体定律、普适气体定律,是描述理想气体在处于平衡态时,压力、体积、温度间关系的状态方程。它建立在玻意耳-马里奥特定律、查理定律、盖-吕萨克定律等定律的基础上,由法国科学家克拉珀龙(Clapeyron)于 1834 年提出,其较为广泛应用的形式见式(1-1):
 (1-1)
(1-1)
式中:p为气体压力(单位为Pa);ρ为气体密度(单位为kmol/m3);R为通用气体常数(单位为kJ/(kmol·K));T为气体温度(单位为K);M为气体的摩尔质量或平均摩尔质量(单位为kg/kmol)。
1873 年,vdW 状态方程诞生,成为首个能预测气液共存的方程。1949 年,Redlich 和Kwong提出了RK状态方程,通过引入温度与引力项(vdW状态方程将压力分为斥力项和引力项两部分)的关系,提高了vdW状态方程的预测精度。1964年,Wilson对RK状态方程中的引力项α进行了温度依赖性的调整。随后,在1972年,Soave对引力项α进行了进一步的修正。1976年,Peng和Robinson提出了RK状态方程的修正项,旨在更精确地预测蒸气压、液体密度和相平衡。在1982年,Patel和Teja对PR状态方程进行了修改,新增了参数c,提出了PT状态方程,从而显著提高了PR状态方程对极性流体和非极性流体的计算精度。
真实流体的维里型状态方程于1885年由Thiesen首次提出,随后,在1901年,Kamerlingh Onnes对维里系数进行了详细的阐释。1928年,Beattie和Bridgeman通过扩展维里项,提出了BB状态方程,该方程在相当长的一段时间内被广泛用于定量描述真实气体的pVT行为,直至其被BWR状态方程所取代。1940年,Benedict等人提出了BWR状态方程,进一步推动了流体状态方程的发展。1971年,Starling提出了11常数方程即BWRS状态方程。1972年,Starling和Han对BWRS状态方程进行了改进,形成了目前广泛应用的BWRSH状态方程。
一些研究者在BWR状态方程的基础上进行了拓展,提出了更为复杂的高精度方程。1962年,Strobridge提出了16常数方程;1970年,Bender提出了20常数方程;1970年,Morsy提出了10常数方程;1973年,Jacobsen和Stewart提出了32常数方程;1975年,Lee和Kesler提出了12常数方程;1975年,Nishiumi和Saito提出了15常数方程;1985年,Schmidt和Wagner提出了32常数方程;1991年,Starling等人提出了53常数方程(AGA天然气方程),为流体状态方程的研究和应用开辟了新的道路。
因为压缩因子是无量纲量,所以可以把它表示为对比温度Tr = T/T *、对比压力pr = p/p*和对比体积Vr = V/V*,其中,T *、p*和V*是物质的特征性质,可以是组分的气-液临界值Tc、pc和Vc(或RTc/pc,以及其他的具有体积单位的量)。通常使用临界温度、临界压力和临界体积来表示对比参数,即对比温度Tr = T/Tc、对比压力pr = p/pc和对比体积Vr = V/Vc。将状态方程写为无量纲函数和无量纲变量的普遍原理的表达式,这个原理称为对比态原理(Principle of Corresponding State,CSP),有的文献中也称为对比态定律。
对比态原理又称对应态原理,物质的物理性质参数是和它的状态(如温度、压力等)有关的,当不同物质在所处状态下的对比压力、对比温度相同时,则称这些物质处于对应状态;当以对比值来表示这些参数时,认为它们之间具有相同的函数关系,这即对比态原理的另一种解释。其一般形式和具体形式都可以由分子理论(Hakala,1967 年)推导。物质的特征参数的数目决定了 CSP 的级别。
二参数CSP指的是,仅用两个特征参数如Tc和pc来使状态无量纲化,无量纲化的函数可以是压缩因子Z,Pitzer(1939 年)和Guggenheim(1945 年)论述了这种最低级别的CSP的分子条件。特征参数为Tc和pc或者Tc和Vc时,只有单原子物质如氩气、氪气、氙气或“简单流体”(Guggenheim,1945年)才精确遵从二参数形式,其他物质都有一些偏离。
一般情况下,好的状态方程都要在所表达的函数中引入一个或多个无量纲特征参数,为了获得较好吻合的液体性质更需如此。为此,第一步要引入一个第三参数,它通常与蒸气压pvp有关,或与临界点(或临界点附近)的某一体积参数有关。这种做法虽然并不是对所有物质都有用,但对许多物质还是能提高精度的。实际上,这种做法的成功可能已超出了预期,分子理论建议,非极性分子非球形的影响和球形性(Globularity)(非极性分子间排斥力的作用范围和强度)的影响应该需要单独的特征参数,但是实际上只用了单个特征参数来同时说明上述两种影响。
历史上,在大约同一时期有几个不同的第三参数被引入,但是被普遍采用的是临界压缩因子 Zc(Lydersen等人,1955年)和偏心因子ω(Pitzer,1955年)。Lydersen等人针对不同的Zc值,对T/Tc和p/pc的每一步增点都用表格列出了Z值和对比热力学性质,后来Hougan等人(1959年)做了改进。
更常用的第三参数是偏心因子 ω。Pitzer的假设是,ω 将以线性(泰勒级数)方式描述与单原子气体的偏差,这意味着所需要的修正很小,而不是用不同的表格来表示增量值。若 ω 不能以线性方式描述,就必须使用非线性项或插值技术。
压缩因子可以写为式(1-2)的形式:
 (1-2)
(1-2)
式中:Z (0)和Z (1)是对比温度和对比压力的通用函数,Z (0)可由单原子类物质得出,将不同物质的(Z−Z (0))/ω加以平均可得到Z (1)。
偏心因子可由实验数据或关联数据得到,它的易得特点和方程形式使它自出现以后就被选为第三参数,并且对它的优先选择还会持续下去。
人们曾一度认为ω仅适用于“标准”物质,而且仅限于ω值偏小的情况(Pitzer,1955年),而不适用于强极性或缔合类(如通过氢键连接)物质。在一系列有关偏心因子何时能被用于描述化合物的讨论中,Pitzer(1955 年)强调表面张力是十分灵敏的性质,可用来指示何时化合物的分子力比“标准”物质的分子力更复杂。表面张力σ的一个方程见式(1-3):
 (1-3)
(1-3)
关于CSP的使用,Pitzer认为如果一个物质对式(1-3)的偏离超过5%,它就“显示了重大反常”,否则,这个物质可以被认为是“标准”的,三参数CSP就应该是可靠的。
ω 的线性变化是否恰当这个问题也一直被讨论,一些关联式如pvp关联式采用二次函数的效果最好(Pitzer和Curl,1955年)。然而,针对所有种类的物质,已经发展了仅基于 ω 的线性变化的许多有用的特征参数和具有其他性质的关联式。在有关化合物不“标准”或 ω 大于0.6的情况下,如没有对偏心因子在某个性质模型或化合物组分的所属种类模型中的正确性进行验证,使用者应谨慎使用偏心因子。
对于多参数CSP,本书不做介绍。
第一个描述气相和液相以及相间转化的方程是1873年提出的著名的vdW状态方程,见式(1-4):
 (1-4)
(1-4)
vdW 状态方程应用于纯组分或压力较低的混合物,它考虑了实际流体中分子占有的体积(排斥体积)和分子吸引力,方程第一项被称为斥力项,第二项被称为引力项,该方程为建立 CSP 和立方型状态方程的发展奠定了基础。
vdW 状态方程被提出后,需要确定方程的参数a、b。第一种方法是通过实验数据拟合,通常使用气相压力和气相或者液相密度;第二种方法是通过纯组分的临界参数和式(1-5)的临界状态确定。
 (1-5)
(1-5)
可以得出式(1-6):
 ,
, 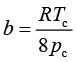 (1-6)
(1-6)
vdW 状态方程预测的流体临界压缩因子为 0.375,但是不同的烃的压缩因子范围为 0.24~0.29。如果考虑非烃类,这个范围要扩大,并且预测蒸气压不精确。于是许多更为精确的方程被提出,其中较为著名的为1949年Redlich和Kwong提出的RK状态方程,见式(1-7):
 (1-7)
(1-7)
RK 状态方程在引力项中引入了温度依赖项和一个稍微不同的体积的关系。与 vdW 状态方程相比,在一定程度上来说,RK 状态方程给出了一个较好的流体临界压缩因子(Zc = 1/3),同时给出了一个较好的第二维里系数,但是RK状态方程在相界和液体密度的预测中仍然不精确。
1964年,Wilson改变了RK状态方程中引力项的温度依赖项,见式(1-8):
 (1-8)
(1-8)
式中:
 (1-9)
(1-9)
 ,
,  (1-10)
(1-10)
1972年,Soave修改了参数α,见式(1-11):
 (1-11)
(1-11)
对参数 α 的修改使得预测轻烃蒸气压(特别是在 0.1MPa 以上)变得精确,这使得立方型状态方程成为预测在中压和高压下非烃类流体的气液平衡的重要工具,修改后的方程被称为SRK状态方程。
1976年,Peng和Robinson使用不同的体积依赖项稍微改善了液体密度(Zc = 0.307)的预测精度,并且通过改变温度依赖项中的参数α来精确预测C6~C10烃类蒸气压,见式(1-12):
 (1-12)
(1-12)
式中:
 (1-13)
(1-13)
1979年,Abbott提出了用5个参数来表示立方型状态方程的通用形式,见式(1-14):
 (1-14)
(1-14)
式中,p为系统压力(kPa);T为系统温度(K);V为流体的摩尔体积(m3/kmol);R为气体常数(kJ/(kmol·K))。参数b、θ、η、δ和ε根据模型而定,可以是常数(包括0),或者是随温度T或组分变化。
式(1-14)可以用式(1-15)表示:
 (1-15)
(1-15)
式(1-15)也可以表示为式(1-16):
 (1-16)
(1-16)
式(1-16)中,定义无量纲参数见式(1-17):
 (1-17)
(1-17)
η一般取值为b,其他常用参数见赵红玲等人翻译的《气液物性估算手册》一书。
维里型状态方程是摩尔体积倒数的无限幂级数项,该方程代表真实流体与理想流体的偏离,是由Thiesen在1885年首先提出来的,见式(1-18):
 (1-18)
(1-18)
式(1-18)是关于理想气体体积倒数的麦克劳林级数,等号右边的每一项是前面各项和的修正。按照1901年Kamerlingh Onnes的建议,系数B、C、D等被称为维里系数,B是第二维里系数,C是第三维里系数,以此类推。从统计学来讲,系数与分子间力有关,如第二维里系数代表两个分子间的相互作用,第三维里系数代表3个分子间的相互作用。对于纯流体,维里系数仅仅是温度的函数。
1969年,Mason和Spurling提出了25℃下氩气的收敛级数,如表 1-1 所示,该表清楚地显示了在此超临界温度下,在1个大气压下第二维里系数可以忽略,在 10 个大气压下第三维里系数可以忽略,在 100 个大气压下第三维里系数不可忽略,在 1000 个大气压下第三维里系数的贡献比第二维里系数的要大,这表明该级数收敛慢,甚至不收敛。
表1-1 25℃下氩气的收敛级数
| 压力(大气压)/atm |
压缩因子Z(1−B/V+C/V2+…(余项)) |
|---|---|
| 1 |
1−0.00064+0.00000+…(+0.00000) |
| 10 |
1−0.00648+0.00020+…(−0.00007) |
| 100 |
1−0.06754+0.02127+…(−0.00036) |
| 1000 |
1−0.38404+0.68788+…(+0.37272) |
1980 年,Dymond 和 Smith 用实验数据编制了第二维里系数和第三维里系数,第二维里系数尤其重要,为混合物状态方程的混合规则公式奠定了基础。在式(1-18)中,当 V 增大时,第三维里系数和更高维里系数比第二维里系数更快减小为0,此时,第二维里系数可以表示为式(1-19):
 (1-19)
(1-19)
同样可以得到第三维里系数和第四维里系数,见式(1-20)、式(1-21):
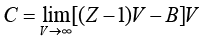 (1-20)
(1-20)
 (1-21)
(1-21)
当V接近无穷大时,p接近0,T为常数,式(1-19)可以转化为式(1-22):
 (1-22)
(1-22)
由式(1-22)可以看出第二维里系数可以通过p、V、T数据作图获得,Z为函数,p为自变量,斜率逐渐变为0。同样,根据玻意耳温度的定义, ,显而易见,第二维里系数在玻意耳温度为 0℃时为 0。各种流体的等温线以及此种类型的数据,被用来发展第二维里系数的关联式。Tsonopoulos(1974年)、Hayden和O'Connell(1975 年)提出的关联式应用十分广泛。Tsonopoulos改善了Pitzer和Curl在1957年提出的非极性流体关联式,Hayden-O'Connell关联式更为复杂,包括偶极矩和回转半径,多应用于各种流体。Tsonopoulos关联式见式(1-23):
,显而易见,第二维里系数在玻意耳温度为 0℃时为 0。各种流体的等温线以及此种类型的数据,被用来发展第二维里系数的关联式。Tsonopoulos(1974年)、Hayden和O'Connell(1975 年)提出的关联式应用十分广泛。Tsonopoulos改善了Pitzer和Curl在1957年提出的非极性流体关联式,Hayden-O'Connell关联式更为复杂,包括偶极矩和回转半径,多应用于各种流体。Tsonopoulos关联式见式(1-23):
 (1-23)
(1-23)
式中:
 (1-24)
(1-24)
1987年,Smith和van Ness提出了更为简单的表达式,其中,第三维里系数的表达式是由Zeller在1970年提出的,1983年,Orbey和Vera对其进行了修正,见式(1-25):
 (1-25)
(1-25)
式中:
 (1-26)
(1-26)
从发展史来说,1901年,Kamerlingh Onnes使用了有限项维里型状态方程来描述阿马加(Amagat)定律的p、V、T数据,但是,他使用的维里型状态方程舍去了第八项后面的项,并且舍去了第三项以后的奇数次幂项来拟合方程,见式(1-27):
 (1-27)
(1-27)
这一方程不再具有维里系数的理论意义,但是简化了曲线拟合参数。特别地, 的值将会随着方程中项数的增减而改变,但是真实第二维里系数不会被其他项所影响。Kamerlingh Onnes为了将维里系数用于对比态原理,使用对比压力(pr = p/pc)、对比温度(Tr = T/Tc)、理想对比体积(Vr = Vpc/(RTc))这些对比态形式表示这一方程。
的值将会随着方程中项数的增减而改变,但是真实第二维里系数不会被其他项所影响。Kamerlingh Onnes为了将维里系数用于对比态原理,使用对比压力(pr = p/pc)、对比温度(Tr = T/Tc)、理想对比体积(Vr = Vpc/(RTc))这些对比态形式表示这一方程。
1928年,Beattie和Bridgeman提出的舍项维里型状态方程是一个令人满意的定量描述真实气体体积的状态方程,见式(1-28)。这一方程被广泛应用于表示气体行为,直到被 BWR 状态方程取代。
 (1-28)
(1-28)
将式(1-28)表示为式(1-29):
 (1-29)
(1-29)
1940年,Benedict、Webb、Rubin修改了BB状态方程,进行甲烷、乙烷、丙烷和正丁烷p、V、T数据的拟合,以便计算高精度密度和其他导出性质,如焓、逸度、蒸气压、蒸发潜热。两年后,他们将该方程应用于这4种轻烃混合物,并在1951年将该方程扩展到正庚烷等8种烃类,见式(1-30):
 (1-30)
(1-30)
将维里型状态方程扩展到无限序列可得到如下方程,见式(1-31):
 (1-31)
(1-31)
尽管BB状态方程和BWR状态方程的前3项维里系数相似,但是BWR状态方程的更为精确,特别是在密相区。
不像 Onnes 或 BB 状态方程都是舍项维里型状态方程,由于 BWR 状态方程包含一个指数项,这一指数项可以扩展为一个关于摩尔体积倒数的无限级数项,所以 BWR 状态方程可以视为一个封闭形式的维里型状态方程。通过表 1-1 可以推测,在密相区和临界区指数项的贡献非常大。
BWR状态方程不仅可以用来表示p、V、T的关系,还可以用来计算气液平衡的k值。
随着BWR状态方程在工程应用中获得广泛接受,其在低温、高密度、临界区和混合物应用中的缺点被发现,方程中常数的专一性和不可获得性也是重要的限制。为了消除这些缺点,许多改进和普适化的BWR状态方程被提出。
原始的BWR状态方程中常数多数是由p、V、T数据确定的,不能给出一个令人满意的代表低于正常沸点的蒸气压,为了改善这一点,许多人提出了修改方程中的温度依赖项。1952年,Bloomer和Rao在BWR状态方程第一温度函数中增加了另外一项即D/T 4,来拟合氮气的数据。1960年,Motard和Organick为氢气添加了关于温度的b和γ函数。1966年Barner和Schreiner,1969年Orye,1971年Starling分别独立构造了关于温度C0的函数,来改善方程在低于正常沸点时的性能。接下来将会讨论其他研究者向温度函数增加附加项来改善包括低温区在内的整个方程的精度。
有两种不同的方法用来改变BWR状态方程在高密度和临界区的精度:一种方法是将pVT空间分为3 个或者 4 个区,然后分别确定每个区的方程常数;另一种方法是增加额外的温度依赖项或/和体积依赖项来增加常数的数量。
1969年,Eubank和Fort将甲烷和乙烷的pVT空间分为4个区,并且确定了每个区的常数来修订API调查项目的44个表格。他们随后使用相同的方法处理其他烃类。这一分区方法早在1958年被Hirschfelder等人使用过。
许多改进的BWR状态方程被提出来后,人们通过增加BWR状态方程的项数来改善整个方程的精度,但是这样也增加了常数的数量。1962年,Strobridge提出来一个改进,见式(1-32):
 (1-32)
(1-32)
这一 16 常数方程为以后的改进树立了榜样,包括Bender在1970年提出的20常数方程、Morsy在1970年提出的10常数方程、Starling在1971年提出的11常数方程、Jacobsen和Stewart在1973年提出的32常数方程、Lee和Kesler在1975年提出的12常数方程、Nishiumi和Saito在1975年提出的15常数方程、Schmidt和Wagner在 1985 年提出的 32 常数方程、Starling 等人在 1991 年提出的 53 常数方程(AGA 天然气方程)。
如图 1-1 所示,增加常数数量或项数通常会改善方程的精度(不同状态方程中可调参数数量与拟合质量之间的关系,以氧气为例),但是对于混合物来说并非经常这样做。
图1-1
最初的混合规则是由Benedict等人在1942年提出来的,见式(1-33),适用于轻烃混合物,但是不适用于含有非烃类的混合物,并且对于烃类混合物也需要做出一些改良。
 (1-33)
(1-33)
1953年,Stotler和Benedict首次提出了使用交互系数mij,等同于(1−Kij),将A0用式(1-34)表示:
 (1-34)
(1-34)
这一混合规则在随后的1969年被Orye用于烃类混合物,1972年Starling和Han将混合规则用于A、C、D、E这4个常数,这些将会在后面进行讨论。
BWR 状态方程的另一个缺点是,在混合物中,当给出不确定的实验数据时,方程中的常数不能唯一确定,因此,可能存在多组常数,这取决于在回归分析中使用的实验数据和权重因子。实际上,不同的研究者对相同的纯流体的常数进行了报道,尽管这些不同的常数在一般情况下符合纯流体的行为,但是对于混合物都可能会给出不同的结果,尤其是当混合规则用于常数数量有较大不同的状态方程计算混合物时候。可以通过对状态方程的参数使用普适化形式来缓解这一问题。
1949年,Joffe首次对BWR状态方程的参数进行了普适化,他按照1901年Kamerlingh Onnes的概念提出了对比形式的BWR状态方程,如将对比压力(pr = p/pc)表达成对比温度(Tr = T/Tc)和理想对比体积(Vr = Vpc/RTc)的函数。通过这一方法,方程变为二参数(pr和Tr)对应态形式,但是并不十分精确。
1955年,Martin和Hou发展了另外一种形式的状态方程,见式(1-35):
 (1-35)
(1-35)
他们报道了二氧化碳、水、苯、氮、硫化氢、丙烷的状态方程的参数,使用温度的指数函数作为参数替代 BWR 状态方程中的多项式。1967 年,Martin 增加了两个额外的指数项——exp(aV)和exp(2aV),来改善方程对于氯二氟甲烷的精确度。
1969年,Vennix和Kobayashi使用另一种形式的维里型状态方程来高精度拟合甲烷密度数据,并且他们使用Martin-Hou形式的温度函数来表示等温线,这一25常数方程见式(1-36):
 (1-36)
(1-36)
1972年,Starling和Han提出了应用更为广泛的普适化方程,他们使用11个参数修改BWR状态方程,使 10 个参数成为偏心因子的线性函数,并且E0为偏心因子的指数函数。在该普适化方程中,他们使用临界密度代替了临界压力。这一无量纲常数方程的简化形式见式(1-37):
 (1-37)
(1-37)
Starling和Han使用了部分最初的BWR状态方程混合规则,改变的混合规则见式(1-38):
 (1-38)
(1-38)
1975 年,Nishiumi和Saito通过增加4个额外的温度依赖项(无量纲常数)来修正Starling-Han方程,以获得对重烃更好的精度,新的 4 个无量纲常数以及它们的混合规则见式(1-39)、式(1-40)。1980年,Nishiumi通过增加极性参数将该方程扩展至极性流体方向。
 (1-39)
(1-39)
 (1-40)
(1-40)
获得普适化方程的一般途径是用对比形式表示BWR状态方程,并且使方程中的常数成为偏心因子的函数。尽管它们是常数,但是通过这一方法,热力学性质均不是偏心因子的线性函数。实际上,不可能使用普适化方程来构造出关于摩尔体积(或压缩因子)和其他衍生属性是偏心因子的线性函数的状态方程。
根据计算的需要以及状态方程参数的实用性,16常数状态方程,例如,Strobridge、Nishiumi和Saito的方程代表了直接应用扩展的维里型状态方程计算混合物实用性上限。尽管更加复杂的状态方程可以用于对比态方法,但这些方程都带有大量的常数,例如接下来要讨论的方程,用来描述纯流体(或者固定成分,如空气或天然气)在一个较宽范围内的条件,包括临界区的p、V、T数据。一旦p、V、T数据被精确地描述,其他热力学属性参数可以由状态方程推导,有时候用表格形式来描述。
Bender提出了一个20常数BWR状态方程用来描述氩、氮、氧、甲烷、氢、乙烷、丙烷的p、V、T数据,见式(1-41)。1977年,Teja和Singh使用同一方程来描述乙烷、丙烷、正丁烷和正戊烷,1980年,Sievers和Schulz使用该方程拟合甲烷数据,他们指出该方程即使有20个常数,但在接近临界区对密度进行预测时偏差仍达4.8%。
 (1-41)
(1-41)
1973年,Jacobsen和Stewart将常数增加至32个,以此将氮气的拟合数据的压力范围提升至1000 MPa,方程见式(1-42):
 (1-42)
(1-42)
这一方程分别被Ely和Magee在1989年、Sherman等人在1989年用来拟合纯二氧化碳和富含二氧化碳的混合物的数据。
Starling 等人在 1991 年为美国天然气研究所开发了天然气方程,该方程就是美国气体协会(AGA)于 1992 年发表的AGA8 报告《天然气和其他烃类气体的压缩性和超压缩性》中提出的压缩因子计算用状态方程,后续经过不断发展,Starling 等人提出了计算天然气和其他相关碳氢化合物气体的气相压缩系数、超压缩系数、密度、比热容、焓、熵、声速等参数的方程。该方程适用于纯甲烷、乙烷、氮气、二氧化碳、氢气和硫化氢以及多达 21 种化合物的气体混合物,目前仍然被国际标准化组织和中国国家标准化管理委员会用于天然气压缩因子计算(ISO 12213-2:2006、GB/T 17747.2—2011)。
在非立方型状态方程中,GERG-2008是一种新型宽范围状态方程,适用于天然气和其他21种天然气成分(甲烷、氮气、二氧化碳、乙烷、丙烷、正丁烷、异丁烷、正戊烷、异戊烷、正己烷、正庚烷、正辛烷、正壬烷、正癸烷、氢气、氧气、一氧化碳、水蒸气、硫化氢、氦气和氩气)的混合物。在整个成分范围内,GERG-2008涵盖这些组分混合物的气相、液相、超临界区域和气液平衡状态,它被认为是适用于需要高精度热力学性质的天然气应用的标准参考方程。GERG-2008的正常有效范围包括90~450K的温度和高达35MPa的压力,有效范围可扩展至从60~700K的温度和高达70MPa的压力。给定的数值信息(包括所有复杂的衍生物)使GERG-2008能够用于各种技术应用。例如,天然气的加工、管道输送或车船运输、储存和液化等。GERG-2008被ISO标准(ISO 20765系列)以及中国国家标准(GB/T 17747.3—2011)采用,该方程的基本形式见式(1-43)。
 (1-43)
(1-43)
式中:a为亥姆霍兹自由能,ρ为混合物密度,T为混合物温度, 为混合物摩尔组分。在给定混合物密度ρ、温度T和摩尔组分
为混合物摩尔组分。在给定混合物密度ρ、温度T和摩尔组分 时,混合物的亥姆霍兹自由能a可以表示为描述理想气体行为的
时,混合物的亥姆霍兹自由能a可以表示为描述理想气体行为的 和描述残余或实际气体贡献的
和描述残余或实际气体贡献的 的总和。
的总和。
Pitzer和其合作者(Pitzer等人,1955年;Pitzer和Curl,1957年、1958年)发展了较好的关联式,将压缩因子和其他热力学参数在给定的对比压力和对比温度下表示为偏心因子的函数,尤其是他们提出了关于压缩因子的表达式,见式(1-44):
 (1-44)
(1-44)
式(1-44)中的 Z (0)是简单流体(ω = 0)的压缩因子,Z (1)是偏离函数,两者均仅为对比压力和对比温度的函数。Lee和Kesler在1975年提出了式(1-45):
 (1-45)
(1-45)
在相同对比状态下,式(1-45)中的Z (0)是简单参考流体(惰性气体,ω = 0)的压缩因子,Z (r)是第二参考流体(正辛烷,ω(r) = 0.3978)的压缩因子。
Lee和Kesler使用改进的BWR状态方程(BWR-Lee-Kesler关联式)的简化形式来表示Z (0)和Z (1),见式(1-46):
 (1-46)
(1-46)
式中:
 (1-47)
(1-47)
简单流体和参考流体的参数见表1-2,混合规则见式(1-48)。
表1-2 简单流体和参考流体的参数
| 参数 |
简单流体 |
参考流体 |
|---|---|---|
| b1 |
0.1181193 |
0.2026579 |
| b2 |
0.265728 |
0.331511 |
| b3 |
0.154790 |
0.027655 |
| b4 |
0.030323 |
0.203488 |
| c1 |
0.0236744 |
0.0313385 |
| c2 |
0.0186984 |
0.0503618 |
| c3 |
0 |
0.016901 |
| c4 |
0.042724 |
0.041577 |
| d1 |
0.0000155488 |
0.0000487360 |
| d2 |
0.0000653920 |
0.00000740336 |
| β |
0.650167 |
1.226 |
| γ |
0.060167 |
0.03754 |
 (1-48)
(1-48)
BWR-Lee-Kesler关联式需要求解两次来获得Vr,第一次求解简单流体的热物性(对比)参数,第二次求解参考流体的热物性(对比)参数。
Lee和Kesler将简单流体和参考流体的prVrTr空间分为一些区,并在每个区为Vr提供关于pr和Tr的函数的简单近似的关联。
为了将BWR-Lee-Kesler关联式用于气液平衡,1976年,Joffe提出了增加BWR-Lee-Kesler关联式的交互系数,1978年,Plocker等人、1981年Oellrich等人也修改了Tcm的混合规则,见式(1-49):
 (1-49)
(1-49)
1982年,Yu等人通过增加修正项至最初的Z (0)(式中为 )来扩展BWR-Lee-Kesler关联式到pr = 100MPa,见式(1-50):
)来扩展BWR-Lee-Kesler关联式到pr = 100MPa,见式(1-50):
 (1-50)
(1-50)
1985年,Wu和Stiel通过使用水作为第二参考流体并且增加其他参数而使BWR-Lee-Kesler关联式用于极性流体,见式(1-51):
 (1-51)
(1-51)
式中:Z(ω)是水的压缩因子;Y是组分特性参数,它取决于偏心因子和极性。随后,Wilding和Rowley在1986年、Wilding等人在1987年也将BWR-Lee-Kesler关联式应用于极性流体。
Teja等人在1980年通过使用第二参考流体替换简单流体的压缩因子而将式(1-45)普适化,见式(1-52):
 (1-52)
(1-52)
式(1-52)中 Z 的表达式基于 Pitzer 的概念,在本质上全部是参考流体的一阶摄动。1984 年,Chung等人使用简单摄动概念将压缩因子表示为各向同性流体的线性组合,见式(1-53):
 (1-53)
(1-53)
式中: 和
和 代表Strobridge修改的BWR状态方程,带有特征能量ε和体积V*的简化形式作为对比参数替代传统的临界温度和临界体积,见式(1-54)。
代表Strobridge修改的BWR状态方程,带有特征能量ε和体积V*的简化形式作为对比参数替代传统的临界温度和临界体积,见式(1-54)。
 (1-54)
(1-54)
式中:y = ρV*,θ = kT/ε,α、ε和V*的值适用于51种物质。如果将式(1-53)和式(1-54)合并,参数A1到A15可以写成式(1-55)的形式。
 (i = 1, 2, …, 15) (1-55)
(i = 1, 2, …, 15) (1-55)
式中:常数B(0)、B(p)和C的值见表1-3。
表1-3 式(1-53)和式(1-54)的参数
| i |
B(0) |
B(p) |
i |
B(0) |
B(p) |
|
|---|---|---|---|---|---|---|
| 1 |
2.5023740 |
0.52182 |
9 |
20.9891320 |
79.29000 |
|
| 2 |
−7.2696120 |
−0.73780 |
10 |
24.7384980 |
6.84750 |
|
| 3 |
−4.5309120 |
−2.56040 |
11 |
36.2897450 |
15.57000 |
|
| 4 |
−1.5257331 |
−5.25270 |
12 |
−207.76901 |
−104.000 |
|
| 5 |
0.3796055 |
−0.12000 |
13 |
1152.75990 |
−435.804 |
|
| 6 |
5.3624275 |
−3.37530 |
14 |
246.49642 |
149.091 |
|
| 7 |
−2.8683227 |
17.10530 |
15 |
229.89942 |
850.000 |
|
| 8 |
15.2886580 |
−19.27400 |
C |
31.6711280 |
||
立方型状态方程也可以表示为以下两种形式,见式(1-56)、式(1-57),其中参数见表1-4。
 (1-56)
(1-56)
 (1-57)
(1-57)
式中:
 (1-58)
(1-58)
表1-4 常用立方型状态方程的参数
| 状态方程 |
u |
ω |
b |
a |
|---|---|---|---|---|
| vdW |
0 |
0 |
|
|
| RK |
1 |
0 |
|
|
| SRK |
1 |
0 |
|
|
| PR |
2 |
−1 |
|
|
RK状态方程的表达式为式(1-59):
 (1-59)
(1-59)
将各参数代入可转化为式(1-60):
 (1-60)
(1-60)
也可以表示为式(1-61)的形式:
 (1-61)
(1-61)
SRK状态方程的表达式为式(1-62):
 (1-62)
(1-62)
将各参数代入可转化为式(1-63):
 (1-63)
(1-63)
也可以表示为式(1-64)的形式:
 (1-64)
(1-64)
PR状态方程的表达式为式(1-65):
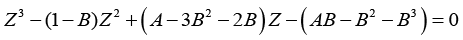 (1-65)
(1-65)
将各参数代入可转化为式(1-66):
 (1-66)
(1-66)
也可以表示为式(1-67)的形式:
 (1-67)
(1-67)
BWRS状态方程可以表示为式(1-68):
 (1-68)
(1-68)
转化为对比态形式,见式(1-69):
 (1-69)
(1-69)
式中:
 (1-70)
(1-70)
Benedict等人在1951年成功将BWR状态方程用于气液平衡计算后,扩展的维里型状态方程成为计算非极性混合物性质的一个重要的、有力的工具。然而,在20世纪70年代中期,SRK状态方程和PR状态方程在气液平衡计算中占主导地位,由于立方型状态方程不能很好地描述体积数据,扩展的维里型状态方程在测定体积和其他需要高精度热力学参数方面仍是首选,烃类气体和液体的密闭输送可能是十分普遍的应用例子。虽然如此,立方型状态方程除了临界区外,在热力学参数的计算中仍然出奇的好。SRK状态方程和PR状态方程有一个共同的问题,对于液体或超临界液体来说在高密度时候都不适应,根本原因在于分子间的作用力。当分子间距离大于平均距离的时候,分子间引力起主要作用,改变分子间的距离只需要很少的能量。一旦分子接触,它们之间的作用力变为斥力,且其大小随距离的减小呈指数级增大,也就是说液体分子几乎是不可压缩的。将分子继续靠近意味着将重组分子,这将会产生很大的斥力。描述随距离减小而迅速增大的分子间斥力,需要有依赖于密度并且比立方型状态方程更有说服力的方程。要得到这种有说服力的方程就需要将维里型状态方程外推出更多的项,这就增加了方程的复杂程度,随之而来的很多系数需要通过数据来验证,这样会造成方程缺少普适性。
在天然气管道模拟中,状态方程的用途如下。
(1)用状态方程通过压力和温度求解密度进行管线充填量(或管存)计算、流量计标定、压力降计算。
(2)计算热力学参数进行热力学建模、压缩机计算、气液平衡计算。
这些用途表明了状态方程应该有以下特点:准确(计量),在很大的压力和温度范围内都适用,可以用于很多组分;精确(热力学),可用于气体和液体的参数计算,使用方便。
通常我们考虑通过以上特点来对状态方程进行对比。由于理想气体的状态方程不能满足或不能精确满足以上特点,所以需要用到实际气体的状态方程。状态方程应该简单、准确,并且可以适用于很大的压力、温度范围和较多的组分,实际上,这样的状态方程是不存在的。有很多只针对一种或几种流体的状态方程,在很大的压力和温度范围内,甚至在接近露点或者临界状态时都很精确,但是这些方程在形式上都很复杂;并且改变组分意味着改变状态方程。
真实的状态方程有很多,本节主要介绍RK、SRK、PR、BWRS和LKP状态方程。
Redlich和Kwong修正了vdW状态方程的压力校正项,并于1949年提出了二参数状态方程,其形式见式(1-71):
 (1-71)
(1-71)
同时给出了该方程的其他形式,见式(1-72):
 (1-72)
(1-72)
本书采用Soave给定的混合规则,a和b采用修正过的数值,见式(1-73):
 (1-73)
(1-73)
式中:p为系统压力(单位为kPa);T为系统温度(单位为K);Tci为临界温度(单位为K);V为流体的摩尔体积(单位为m3/kmol);R为通用气体常数(单位为kJ/(kmol·K))。
参数a、b为两个特性参数,各种组分有不同的参数值,其中,a表示分子间引力,b表示分子大小。参数a、b最好直接根据实验数据拟合求得,但在缺乏实验数据时,可利用临界等温线所具有的特性确定。对于单一组分: ,
, 。其中,Ωa和Ωb为无量纲常数:Ωa = [9 × (21/3 − 1)]−1 ≈ 0.4274802,Ωb = (21/3 − 1)/3 ≈ 0.08664035。更准确的Ωa和Ωb值可由各组分饱和蒸气压的p、V、T数据定出。
。其中,Ωa和Ωb为无量纲常数:Ωa = [9 × (21/3 − 1)]−1 ≈ 0.4274802,Ωb = (21/3 − 1)/3 ≈ 0.08664035。更准确的Ωa和Ωb值可由各组分饱和蒸气压的p、V、T数据定出。
对于混合气体,采用混合规则,见式(1-74):
 (1-74)
(1-74)
RK 状态方程使用方便,计算结果较为精确,许多学者试图加以改进以提高其准确性,特别期望改进后可以计算气液平衡。其中,Soave在1972年提出的改进式简称SRK状态方程,在不失RK状态方程简单的形式下,大大改善了计算气、液相逸度的效果。
Soave 指出,RK 状态方程虽然应用于纯组分及混合物的比热容等的计算时可以获得相当准确的结果,但应用于多组分气液平衡计算时其准确性通常很差。Soave 认为这不能仅归因于 RK 状态方程所用的混合规则尚有缺点,实际上将原先的 RK 状态方程应用于纯组分饱和蒸气压的预测时其准确性也很差,其主要原因在于原先的 RK 状态方程未能如实地反映温度的影响。
Soave对RK状态方程的改进着眼于使之能准确地描述纯组分的饱和蒸气压及气液平衡,据此Soave将RK状态方程中a/T 0.5项改用较具普遍意义的温度函数α(T )来代替,见式(1-75):
 (1-75)
(1-75)
a和b采用修正过的数值,见式(1-76):
 (1-76)
(1-76)
式(1-75)、式(1-76)中的 即式(1-77)中的
即式(1-77)中的 ,是与气体温度和偏心因子ω有关的无量纲因子,按式(1-77)计算:
,是与气体温度和偏心因子ω有关的无量纲因子,按式(1-77)计算:
 (1-77)
(1-77)
对于氢气,见式(1-78):
 (1-78)
(1-78)
对于混合气体,除了考虑各组分i的常数ai和摩尔体积分数yi外,为了改进对非烃-烃体系的预测,Soave在参数a的混合规则中引入经验校正因子(也称为交互系数)Kij,混合规则见式(1-79):
 (1-79)
(1-79)
式(1-75)~式(1-79)中:p为系统压力(单位为kPa);T为系统温度(单位为K);Tci为临界温度(单位为 K);Tri为对比温度,Tri = T/Tci,量纲为 1;V 为流体的摩尔体积(单位为m3/kmol);yi、yj为纯组分的摩尔体积分数;R为通用气体常数(单位为kJ/(kmol·K))。常用气体组分临界参数见表1-5。
表1-5 常用气体组分临界参数
| 气体组分 |
临界温度/℃ |
临界压力/kPa |
偏心因子 |
|---|---|---|---|
| CH4 |
−82.45 |
4640.68 |
0.011498 |
| C2H6 |
32.28 |
4883.85 |
0.0986 |
| C3H8 |
96.75 |
4256.66 |
0.1524 |
| i-C4H10 |
134.95 |
3647.62 |
0.18479 |
| n-C4H10 |
152.05 |
3796.62 |
0.201 |
| i-C5H12 |
187.25 |
3333.59 |
0.22224 |
| n-C5H12 |
196.45 |
3375.12 |
0.25389 |
| n-C6H14 |
234.75 |
3031.62 |
0.3007 |
| n-C7H16 |
267.01 |
2736.78 |
0.34979 |
| n-C8H18 |
295.45 |
2496.62 |
0.4018 |
| n-C9H20 |
321.45 |
2300.07 |
0.44549 |
| n-C10H22 |
344.45 |
2107.55 |
0.48848 |
| N2 |
−146.96 |
3394.37 |
0.04 |
| CO2 |
30.95 |
7370.00 |
0.23894 |
| H2S |
100.45 |
9007.79 |
0.081 |
| He |
−267.96 |
226.97 |
−0.390032 |
Kij的值需由混合物中二元系的气液平衡数据确定。对于烃-烃体系,Kij = 0。对于非烃类气体和烃类气体间的Kij,Kji = Kij。PR和SRK状态方程中常用气体的二元交互系数Kij见表1-6,摩尔质量见表1-7。
Peng和Robinson指出,经Soave改进的SRK状态方程虽然取得了明显进步,但仍有一些不足之处,例如 SRK 状态方程对液相密度的预测准确性欠佳——对烃类组分(甲烷除外)预测的液相密度普遍小于实验数据。对于所有流体来讲,RK和SRK状态方程的通用临界压缩因子Zc = l/3,这个值远大于实际流体的临界压缩因子。为了消除上述不足,Peng和Robinson对SRK状态方程基进行了修正,提出了PR状态方程,见式(1-80):
 (1-80)
(1-80)
对于单一组分,见式(1-81)、式(1-82):
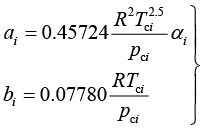 (1-81)
(1-81)
 (1-82)
(1-82)
混合规则见式(1-83):
 (1-83)
(1-83)
式(1-80)~式(1-83)中:p为系统压力(单位为kPa);T为系统温度(单位为K);Tci为临界温度(单位为 K);Tri为对比温度,Tri = T/Tci,量纲为 1;V 为流体的摩尔体积(单位为m3/kmol);yi、yj为纯组分的摩尔体积分数;R为通用气体常数(单位为kJ/(kmol·K))。
目前各文献中PR状态方程的形式有几十种之多,方程中系数ai、bi和αi的具体形式也有所差异。此外,各文献中采用的流体物性参数也有所不同,且二元交互系数不完整,因此计算结果存在差异。本书采用的临界参数、二元交互系数Kij和摩尔质量分别见表1-5~表1-7。
BWRS状态方程是通过修正BWR状态方程而得到的,它保留了BWR状态方程中与密度关联的项,改变了与温度关联的项。BWRS状态方程包含计算轻烃组分的系数和决定烃类混合物气体系数的混合规则,它可以用于热力学参数计算和气液平衡计算。
由于BWRS状态方程能够用于计算气液平衡,其方程系数可以由公式算得,并且有适用于很多烃类的混合规则。
BWRS状态方程是一个多参数状态方程,其基本形式见式(1-84)、式(1-85):
 (1-84)
(1-84)
 (1-85)
(1-85)
式中:p为系统压力(单位为kPa);T为系统温度(单位为K);ρ为流体的密度(单位为kmol/m3);R为通用气体常数(单位为kJ/(kmol·K))。
A0i、B0i、C0i、D0i、E0i、ai、bi、ci、di、αi、γi这11个参数可以由临界温度Tci、临界密度ρci及偏心因子 ωi的关联式求得,见式(1-86):
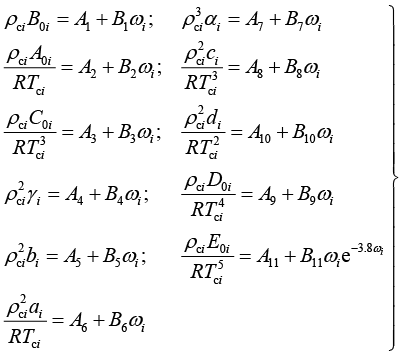 (1-86)
(1-86)
式中:Ai、Bi(i = 1, 2, 3, ···, 11)为通用常数,见表1-8。
Starling 在 1973 年、1977 年分别给出了方程中多个物质的 11 个参数(A0i、B0i、C0i、D0i、E0i、ai、bi、ci、di、αi、γi),见表1-9和表1-10。对于纯组分的这11个参数可引用经过单位制转换后的Starling的文献中的数据,而不必使用关联式求解。
对于混合物,BWRS状态方程应采用如下混合规则进行计算,见式(1-87):
 (1-87)
(1-87)
式中:yi为气相或液相混合物中组分i的摩尔分数;Kij(Kij = Kji)为组分i、j间交互系数。
Kij表示和理论混合物的偏差,Kij越大,说明偏差越大。对于同一组分,Kij = 0。Starling给出了18种常见组分间的Kij数据。
Starling提供了纯物质的临界参数和普适化系数。一旦知道对流体所附加的系数值(如临界参数、分子量等),所有的状态参数都可以用已知的状态来计算。但是,很多流体模型通过流动方程来计算压力和温度,而用状态方程来计算密度。由于 BWRS 状态方程中密度是隐式的,需要通过迭代来计算,这样在大型管网计算中会花很多时间来计算密度。本书将在后面探讨密度和压缩因子的快速算法。
Plocker等人发现BWR-Lee-Kesler关联式的混合规则仅适用于含有小的非极性分子的混合物,为了将其推广到含H2S、CO2和H2等组分、具有较高沸点的非极性或弱极性混合物,他们在1978年提出了LKP状态方程,并将该方程推广到由小分子(如N2、CO、CH4和H2)和大分子(如高沸点的烷烃、芳烃和稠环化合物)组成的不对称混合物的气液平衡和焓的计算中。LKP状态方程保留了 LK 状态方程的形式,修改了混合规则,增加了两个参数 Kij和 η。二元交互系数Kij可由纯组分的临界参数关联得到。对于参数η,对称混合物的η = 0,稍微不对称混合物的η = 1,严重不对称混合物的η = 0.25。Kij和η的引入提高了方程的精度。LKP状态方程及其混合规则见式(1-88):
 (1-88)
(1-88)
式中:Z为压缩因子,ω为偏心因子,pr为对比压力,Vr为对比摩尔体积,Tr为对比温度,上标(0)表示简单流体的相应参数,上标(r)表示参考流体的相应参数,其余参数为常数。
LKP状态方程的参数见表1-2。
对于混合物,虚拟临界性质(又称为假临界性质)的表达式见式(1-89):
 (1-89)
(1-89)
式中:Kij为二元交互系数,见表 1-11;η 为虚拟临界温度混合规则中的通用指数,取值为0.25。
表1-11 LKP状态方程中的Kij参数
| 组分 |
甲烷 |
乙烷 |
丙烷 |
异丁烷 |
正丁烷 |
异戊烷 |
正戊烷 |
正己烷 |
正庚烷 |
正辛烷 |
异辛烷 |
正壬烷 |
正癸烷 |
正十一烷 |
碳七+ |
氮气 |
一氧化二氮 |
一氧化碳 |
二氧化碳 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 |
C2 |
C3 |
i-C4 |
n-C4 |
i-C5 |
n-C5 |
n-C6 |
n-C7 |
n-C8 |
i-C8 |
n-C9 |
n-C10 |
n-C11 |
C7+ |
N2 |
N2O |
CO |
CO2 |
|
| 甲烷 |
1 |
1.052 |
1.113 |
1.155 |
1.171 |
1.228 |
1.24 |
1.304 |
1.367 |
1.423 |
1 |
1.484 |
1.533 |
1 |
1 |
0.977 |
1 |
1 |
0.975 |
| 乙烷 |
1.052 |
1 |
1.01 |
1.036 |
1.029 |
1.07 |
1.064 |
1.106 |
1.143 |
1.165 |
1 |
1.214 |
1.237 |
1 |
1 |
1.082 |
1 |
1 |
0.938 |
| 丙烷 |
1.113 |
1.01 |
1 |
1.003 |
1.003 |
1.009 |
1.006 |
1.047 |
1.067 |
1.09 |
1 |
1.115 |
1.139 |
1 |
1 |
1.177 |
1 |
1 |
0.925 |
| 异丁烷 |
1.155 |
1.036 |
1.003 |
1 |
1.001 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.946 |
| 正丁烷 |
1.171 |
1.029 |
1.003 |
1.001 |
1 |
0.998 |
0.994 |
1.018 |
1.027 |
1.046 |
1 |
1.064 |
1.078 |
1 |
1 |
1.276 |
1 |
1 |
0.955 |
| 异戊烷 |
1.228 |
1.07 |
1.009 |
1 |
0.998 |
1 |
0.987 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 正戊烷 |
1.24 |
1.064 |
1.006 |
1 |
0.994 |
0.987 |
1 |
0.996 |
1.004 |
1.02 |
1 |
1.003 |
1.045 |
1 |
1 |
1.372 |
1 |
1 |
1.002 |
| 正己烷 |
1.304 |
1.106 |
1.047 |
1 |
1.018 |
1 |
0.996 |
1 |
1.008 |
1.005 |
1 |
1.015 |
1.025 |
1 |
1 |
1.442 |
1 |
1 |
1.018 |
| 正庚烷 |
1.367 |
1.143 |
1.067 |
1 |
1.027 |
1 |
1.004 |
1.008 |
1 |
0.993 |
1.002 |
1.002 |
1.01 |
1 |
1 |
1 |
1 |
1 |
1.058 |
| 正辛烷 |
1.423 |
1.165 |
1.09 |
1 |
1.046 |
1 |
1.02 |
1.005 |
0.993 |
1 |
1 |
0.993 |
0.999 |
1 |
1 |
1 |
1 |
1 |
1.09 |
| 异辛烷 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.002 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 正壬烷 |
1.484 |
1.214 |
1.115 |
1 |
1.064 |
1 |
1.033 |
1.015 |
1.002 |
0.993 |
1 |
1 |
0.991 |
1 |
1 |
1 |
1 |
1 |
1.126 |
| 正癸烷 |
1.533 |
1.237 |
1.139 |
1 |
1.078 |
1 |
1.045 |
1.025 |
1.01 |
0.999 |
1 |
0.991 |
1 |
1 |
1 |
1 |
1 |
1 |
1.16 |
| 正十一烷 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 碳七+ |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 氮气 |
0.977 |
1.082 |
1.177 |
1 |
1.276 |
1 |
1.372 |
1.442 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.073 |
0.987 |
1.11 |
| 一氧化二氮 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.073 |
1 |
1 |
1 |
| 一氧化碳 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.987 |
1 |
1 |
1 |
| 二氧化碳 |
0.975 |
0.938 |
0.925 |
0.946 |
0.955 |
1 |
1.002 |
1.018 |
1.058 |
1.09 |
1 |
1.126 |
1.16 |
1 |
1 |
1.11 |
1 |
1 |
1 |
| 硫化氢 |
1 |
1 |
1 |
0.947 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.983 |
1 |
1 |
0.922 |
| 氢气 |
1.216 |
1.604 |
1.826 |
2.093 |
2.335 |
2.456 |
2.634 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.08 |
1 |
1 |
1.624 |
| 水 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.92 |
| 氦气 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 氩气 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.988 |
1 |
1 |
1 |
| 氧气 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.997 |
1 |
1 |
1 |
| 氨气 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.033 |
1 |
1 |
1 |
| 苯 |
1.234 |
1.066 |
1.011 |
1 |
0.999 |
1 |
0.977 |
0.978 |
0.985 |
0.987 |
0.982 |
1.034 |
1.047 |
1 |
1 |
1 |
1 |
1 |
1.018 |
| 甲苯 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 乙烯 |
1.014 |
0.991 |
1 |
1 |
0.998 |
1 |
1 |
1 |
1.163 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 丙烯 |
1.089 |
1.002 |
0.992 |
1.009 |
1.01 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.151 |
1 |
1 |
1 |
| 环己烷 |
1.269 |
1.081 |
1.037 |
1 |
1.008 |
1 |
0.996 |
0.998 |
0.999 |
1.01 |
1 |
1.021 |
1.032 |
1 |
1 |
1 |
1 |
1 |
1.054 |
| 乙炔 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 异丁烯 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 二氟二氯甲烷 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.969 |
| 甲醇 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.069 |
| 硫化氢 |
氢气 |
水 |
氦气 |
氩气 |
氧气 |
氨气 |
苯 |
甲苯 |
乙烯 |
丙烯 |
环己烷 |
乙炔 |
异丁烯 |
二氟二氯甲烷 |
甲醇 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H2S |
H2 |
H2O |
He |
Ar |
O2 |
NH3 |
C6H6 |
C7H8 |
C2H4 |
C3H6 |
C6H12 |
C2H2 |
i-C4H8 |
R-12 |
CH3OH |
| 1 |
1.216 |
1 |
1 |
1 |
1 |
1 |
1.234 |
1 |
1.014 |
1.089 |
1.269 |
1 |
1 |
1 |
1 |
| 1 |
1.604 |
1 |
1 |
1 |
1 |
1 |
1.066 |
1 |
0.991 |
1.002 |
1.081 |
1 |
1 |
1 |
1 |
| 1 |
1.826 |
1 |
1 |
1 |
1 |
1 |
1.011 |
1 |
1 |
0.992 |
1.037 |
1 |
1 |
1 |
1 |
| 0.947 |
2.093 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.009 |
1 |
1 |
1 |
1 |
1 |
| 1 |
2.335 |
1 |
1 |
1 |
1 |
1 |
0.999 |
1 |
0.998 |
1.01 |
1.008 |
1 |
1 |
1 |
1 |
| 1 |
2.456 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
2.634 |
1 |
1 |
1 |
1 |
1 |
0.977 |
1 |
1 |
1 |
0.996 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.978 |
1 |
1 |
1 |
0.998 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.985 |
1 |
1.163 |
1 |
0.999 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
0.987 |
1 |
1 |
1 |
1.01 |
1 |
1 |
1 |
1 |
|
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.982 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.034 |
1 |
1 |
1 |
1.021 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.047 |
1 |
1 |
1 |
1.032 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 0.983 |
1.08 |
1 |
1 |
0.988 |
0.997 |
1.033 |
1 |
1 |
1 |
1.151 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 0.922 |
1.624 |
0.92 |
1 |
1 |
1 |
1 |
1.018 |
1 |
1 |
1 |
1.054 |
1 |
1 |
0.969 |
1.069 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.094 |
1 |
0.979 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.094 |
1 |
1 |
1 |
1 |
0.948 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.006 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.979 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.948 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1.006 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |