轻轻松松学会微积分

轻轻松松学会微积分/（英）西尔维纳斯·菲利普斯·汤普森（Silvanus Phillips Thompson），（美）马丁·加德纳（Martin Gardner）著；涂泓，冯承天译.北京：人民邮电出版社，2025.--（欢乐数学营）.ISBN　978-7-115-65724-4

中国国家版本馆CIP数据核字第2024GV6122号

Published by arrangement with St. Martin's Publishing Group.

◆著　[英]西尔维纳斯·菲利普斯·汤普森（Silvanus Phillips Thompson）　[美]马丁·加德纳（Martin Gardner）

译　涂泓　冯承天

责任编辑　刘朋

责任印制　陈犇

◆人民邮电出版社出版发行　　北京市丰台区成寿寺路11号

邮编　100164　　电子邮件　315@ptpress.com.cn

网址　https://www.ptpress.com.cn

文畅阁印刷有限公司印刷

开本：720×960　1/16

印张：20.75　　2025年6月第1版

字数：298千字　　2025年6月河北第1次印刷

内容提要

许多人认为，对于学习数学的学生来说，微积分是一门具有很大挑战性的科目。这本经典图书将改变你对微积分的这种认识，帮助你轻松掌握微积分的基础知识。

本书最初由英国皇家学会会员、物理学家和科学史学家西尔维纳斯·菲利普斯·汤普森撰写，后来经过数次修订和完善，其中最近一次由美国著名数学家、科普作家马丁·加德纳完成。作者采用通俗易懂的语言，生动形象地阐述了微积分的基本原理和实际意义，并通过丰富的实例介绍了微积分的基本计算方法和应用技巧。本书主要内容包括函数、极限和导数的概念，小量的比较，常量的处理，和、差、积、商的导数，高阶导数，导数的几何意义，极大值和极小值，曲线的曲率，部分分式和反函数，正弦函数和余弦函数的处理，偏导数，积分以及微分方程的求解等。

本书可作为高中生和大学生学习微积分的入门读物，也可供数学爱好者阅读。

译者序

作为数学的一个重要分支，微积分在物理学、天文学、生物学、经济学等领域的应用日益显现出其无可替代的价值。与此同时，微积分作为大学的一门基础课程，却常常令学生感到头疼不已。哪怕是在像物理学这样严重依赖微积分的专业，学生最初对微积分的反应也并不是赞叹它有用，而是抱怨它难以入门。这是相当令人震惊和失望的。

由于微积分的基础地位，这门课程通常会被安排在专业课程之前进行学习。在刚进入大学接触微积分时，有的学生甚至发出了这样的感慨：“微积分使我的人生变得艰辛了。”他们对此给出的理由是这门课程“太抽象”。等到在专业课上需要用到微积分这一武器时，学生本应已经拥有了整个武器库，但他们看着“连续质量分布”“连续带电体”等各种巴巴爸爸式的概念一筹莫展。学生通过专业课的学习逐渐习惯了微积分的应用后，又会如梦初醒般地体会到“微积分确实很有用，以前觉得不可能解决的问题现在都能解决了”，甚至对微积分产生了深深的敬意。

由此产生的启示是：既然从应用中学习更能让学生掌握微积分的基本原理，也更能让学生体会到微积分的巨大作用，那么我们为什么不能一开始就通过实际应用来教授微积分呢？想来这大概是因为目前大多数微积分教科书和高等数学教科书出自数学家之手，而数学家往往追求证明的严密和体系的完整，而对于理论的应用不甚关心。所以，对于大多数不太关心证明过程而更注重实际应用的专业的学生而言，这些教科书常常显得过于抽象，因而也就难以理解了。

相比之下，本书的主要作者西尔维纳斯·菲利普斯·汤普森是英国的一位物理学家和科学史学家，他在电气、机械、光学和X射线等领域都颇有造诣，做出过不少重要贡献。本书正是一本注重实际应用的微积分启蒙读物，在1910年首次出版以后立即受到了全球读者的欢迎，多次再版，销量早已超过百万册。

本书从最基本的概念入手，对知识点进行详细拆解，逐步引导读者步入微积分的殿堂。作者始终强调化繁为简，用简洁的语言和生动的实例阐释抽象的公式和定理，使读者在阅读过程中感受到微积分的魅力。例如，在讲到二阶小量时，他用时间和金钱举例，通过具体的数值，让读者理解为什么像x⋅dx,x2⋅dx,ax⋅dx这样的量不能忽略不计，但dx⋅dx是可以忽略不计的。在讲到导数时，作者指出

只是一个简单的比例，也就是dy和dx都趋于无穷小时的比，并通过一架靠在墙上的梯子说明当x与y具有函数关系时

的意义是什么。在此基础上，作者继续从几何角度进行阐述：假设一个正方形的边长为x，倘若将这个正方形的各个边长都增加一个很小的量dx，从而放大这个正方形，那么该正方形的面积就从x2增大到了(x+dx)2，即增大了2x·dx+dx·dx，而其中dx·dx是一个二阶小量，可以忽略。于是，读者就逐渐理解了为什么

。

书中的每一章都以这种方式拆解一个知识点，从真实的例子、函数图像、几何图形等角度逐步深入。在每引入一个知识点后，作者都会及时地提供一些应用实例，帮助读者理解刚刚学过的新知识。这些例子包括圆柱体的体积关于其半径的变化率、费里辐射高温计的灵敏度、复利计算、介质对光的吸收、放射性衰变等。这些实例使读者不仅能加深对新技巧的理解，还能体会到相关技巧的用途，并得到一些实际操作经验。

在大部分章的最后，作者还提供了一些与本章相关的练习题。这些练习题同样注重应用，例如铁棒的热胀冷缩、白炽灯的发光强度随电压的变化、导线的电阻与温度的关系、上升过程中气球的运动、石块落水后的运动等。读者可以通过这些练习题巩固新学的知识，并根据书后提供的答案来了解自己的学习情况。

虽然本书的涵盖面广，包括微分、积分、曲率、极值、微分方程等微积分的基本内容，但作者从结构上将这些知识详细分解为23章，便于读者阶段性地学习。此次中译本是根据1998年的修订版译出的，我国读者非常熟悉的美国著名数学家、科普作家马丁·加德纳对此版做了全面的修订和完善，撰写了序言，并增加了预备知识（函数、极限和导数的概念），从而使本书更加适合从零开始学习微积分的读者阅读。在翻译过程中，我们尽量贴近原著的表述方式和写作风格，并做了少量注释。

感谢人民邮电出版社的工作人员，他们的辛勤工作使得这部经典著作得以以中文版的形式与广大中国读者见面。感谢烟台大学的朱用文教授，他不辞辛劳，认真细致地审阅了译文，并提出了许多宝贵的建议。我们相信，《轻轻松松学会微积分》中文版的出版将有助于更多的中国读者掌握微积分这一强大的工具，并将其应用于各自的领域之中。

编者的话

这是一部经典著作，自首次出版至今已有100多年，深受读者喜爱，在帮助初学者学习微积分的过程中发挥了积极作用。此次中文版的出版旨在为国内读者提供一本有价值的参考书。为了帮助读者更好地使用本书和学习微积分，提请读者注意以下几点。

这本书的重点是介绍微积分的基本原理、计算方法和应用技巧，因此汤普森有意回避了极限概念，以减轻初学者的负担。加德纳根据现代学习的需要补充了极限的部分内容，如果读者想进一步了解极限的更多知识，请参阅相关图书。

作为本书的另一个特色，汤普森用一种直观的方法来讲解积分的概念，而且该方法将不定积分和定积分似乎统一起来了。在一些具体的例子，比如计算长度和面积的部分例题中，书中采用同一个数学符号，既表示不定积分，又同时表示定积分，也就是说汤普森并没有十分严格地区分不定积分与定积分。这与现代数学教科书的做法不完全一致，初学者还是应该严格区分这两个概念的。

此外，为了完全聚焦于微分与积分的计算，作者没有对连续、可导、可微等概念进行过多的介绍，也没有讨论其相关关系。初学者不要因此而产生错觉，以为所有的函数都是连续、可导或者可微的。我们从一开始就要有一个正确的认识，那就是函数并不总是连续的，也并不总是可导或者可微的。当然，这三个概念也是彼此不同的，连续并不意味着可导或可微，可微与可导也是有区别的。

在出版过程中，我们尽力呈现原著的风格和特色，仅在体例上进行了一些必要的调整，并修正了原著中的少量差错。原著中的一些实例采用了英寸、英尺、码、英里、海里等非国际单位制单位[1]，对这些单位的换算反而会影响读者阅读和学习，因此我们在中译本中予以保留。在讲解有关例题和习题时，作者并未十分关注单位的规范使用，也未严格区分等号和约等号。虽然这并不影响读者对微积分原理和应用的理解与掌握，但我们在中译本中还是尽量予以补充和完善。如有不妥之处，欢迎指出。

总之，本书是初学者进入微积分殿堂的一本不可多得的入门书，并且经过了长时间的检验，值得推荐。

[1].1英寸 = 2.54厘米，1英尺 = 12英寸 = 0.3048米，1码 = 3英尺 = 0.9144米，1英里 = 5280英尺=1609.344米。在英国，1海里 = 1853.181米，而大多数国家定义1海里为1852米。——编者

1998年版序言

美国的大学新生和部分高中生需要学习微积分的一些入门课程。对于那些希望成为数学家或者想从事需要微积分知识的职业的学生来说，这类课程是他们必须跨越的最大障碍。研究表明，在修读微积分课程的大学新生中，几乎有一半会通不过。这些没有通过的学生几乎总是会放弃主修数学、物理学或工程的计划，因为在这三个领域中，微积分是必不可少的。他们甚至可能决定不学习诸如建筑、行为科学和社会科学（尤其是经济学）这样的专业，因为微积分在这些专业中是有用的。他们离开了他们担心会太难走的道路，转而去考虑从事那些比较简单的职业。

退出率如此之高的一个原因是微积分入门课程教得实在太差了。课上得往往太无聊，以至于学生们有时会打瞌睡。微积分教科书一年比一年厚，加上了更多计算机绘制的图形和著名数学家的照片（以牛顿和莱布尼茨打头），但这些书似乎从来没有变得更容易理解。你徒劳地翻看它们，想寻找简单、清晰的阐述和能引起你的兴趣的问题，但一无所获。正如一位数学家最近所说的，这些书中的练习具有“解答填字游戏的尊严”。美国的现代微积分教科书通常有1000多页，足以当作门挡用，还有1000多道令人生畏的练习题！它们的价格正在迅速逼近100美元。

“为什么微积分教科书这么重？”林恩·阿瑟·斯蒂恩在一篇题为《微积分改革者的20个问题》（Twenty Questions for Calculus Reformers）的论文中问道，这篇论文转载于罗纳德·道格拉斯主编的《迈向精简而生动的微积分》（Toward a Lean and Lively Calculus，美国数学学会，1986年）一书。他回答道：“出版者在经济上的考量迫使作者……加入每一个人可能想要的每一个主题，这样就不会有人因为遗漏了某项内容而不购买这本教科书。这样做的结果就是微积分教科书变成了一本包含技巧、例题和练习题的百科全书式的汇编，它更像一本臃肿的练习册，而不再是对一个宏伟主题的启发性介绍。”

斯蒂恩是圣奥拉夫学院的一位数学家，他后来宣称：“微积分教学是这个国家的耻辱。很多时候，微积分是由缺乏经验的教师在一个反馈不足的环境中教授给准备不足的学生们的。”

伦纳德·吉尔曼在《大学教学丑闻》［The College Teaching Scandal,《焦点》（Focus），第8卷，1988年，第5页］中写道：“微积分的处境多年来一直很糟糕，考虑到我们这个职业的惰性，这种状况很可能还会持续很久。”

微积分被称为数学家们最不喜欢教授的科目。我们希望只有那些没有领会到其巨大的力量和美的教师才是这样。霍华德·伊夫斯是一位已经退休的数学家，他实际上很喜欢教授微积分。在他的《数学史上的里程碑》（Great Mo‐ments in Mathematics）一书中，我读到了这样一段话：

当然，在大学低年级的数学课程中，没有哪个科目比微积分教起来更令人兴奋或更有乐趣了。教授微积分就像在著名的三环大马戏团当领班一样。据说，人们可以在大学校园里认出那些已学习过微积分的学生——这些学生都没有眉毛。由于对这个科目令人难以置信的广泛应用感到非常惊讶而常常扬起眉毛，因此学习微积分的那些学生的眉毛就变得越来越高，最终消失在他们的后脑勺。

近年来，数学界对改进微积分教学方法的议论很多，会议开得无休无止，其中许多会议是由美国政府资助的。数十个试验项目正在各地开展。

一些改革的领导者认为，尽管传统教科书越来越厚，但对高等微积分的需求实际上正在减少。伊夫斯在他广受欢迎的《数学史导论》（Introduction to the History of Mathematics）一书中伤感地写道：“如今，数学的大部分与微积分或其扩展没有联系，或者几乎没有联系。”

为什么会这样？其中一个原因是显而易见的。计算机！现今数字计算机的运算速度和功能已经变得令人难以置信。以前只能用慢速的模拟计算机处理的连续函数现在可以转化成离散变量函数，再由数字计算机通过逐步算法有效地进行处理。一个过于复杂而无法用铅笔在绘图纸上绘制的函数图像，用一台称为图形计算器的手持式计算器就能立即显示出来。现在的趋势是从连续数学转向过去所谓的有限数学，但现在人们更常称之为离散数学。

微积分正在稳步降级，让位给组合学、图论、拓扑学、扭结理论、群论、矩阵理论、数论、逻辑学、统计学、计算机科学以及其他一系列连续性在其中起着相对次要作用的学科。

离散数学无处不在，不仅在数学领域，在科学和技术领域也是如此。量子理论中充满了离散数学，甚至空间和时间也可能被量子化。演化是通过离散的突变进行的。电视信号即将用离散数字传输方式取代连续模拟传输方式[1]，从而大大提升画面质量。保存一幅画或录下一首交响乐的最合适的方法是将其转换为离散的数字，这些数字可以永远保存而不会受到损坏。

上高中的时候，我必须掌握一种用纸和笔计算平方根的方法。令人高兴的是，没人强迫我学习如何求立方根和更高次方根！如今已经很难找到记得如何计算平方根的数学家了。他们为什么要记得呢？只要按几个键，就能求出任何数的n次方根，而所需的时间比查阅一本带有n次方根表格的书还短。曾经用来计算巨大数字相乘的对数，现在就像计算尺一样已经过时了。

微积分也面临类似的局面。如今，学生们看不出有什么理由需要掌握烦琐的手算微分和积分的方法，因为计算机可以像计算n次方根、大数相乘和大数相除一样快速完成这类工作。例如，斯蒂芬·沃尔弗拉姆开发的一款被广泛使用的软件Mathematica可以在瞬间求解数学和其他科学领域中出现的微积分问题，并绘制相关的图像。具有求导键和积分键的计算器现在比大多数微积分教科书还便宜。据估计，那些大部头教科书中90%以上的练习题都可以用这种计算器来解答。

微积分改革的领导者并不是建议不再教授微积分，而是建议将重点从解题转移到理解计算机在求解微积分问题时做些什么，因为计算机可以更快、更准确地解题。就算我们只是要知道该让计算机做什么，微积分知识实际上也是必不可少的。最重要的是，微积分课程应该让学生逐渐意识到微积分知识的丰富和优雅。

尽管关于如何改进微积分教学的建议很多，但普遍的共识尚未形成。一些数学家建议在介绍微分之前先引入积分。一个值得注意的范例是理查德·库朗[2]撰写的两卷本经典著作《微分与积分》（Differential and Integral Calculus）。然而，掌握微分要比掌握积分容易得多，所以这种转换还没有流行起来。

多位微积分改革者，特别是托马斯·W．塔克［参看他发表在《美国数学月刊》（American Mathematical Monthly，第104卷，1997年3月，第231～240页）上的《重新思考微积分中的严格性》（Rethinking Rigor in Calculus）一文］建议微积分教科书用增函数定理（increasing function theorem,IFT）取代重要的中值定理（mean value theorem,MVT）。（关于中值定理，请参阅我为本书第10章所写的附注。）增函数定理指出，如果一个函数在某个区间上的导数等于或大于零，那么该函数在这个区间上是递增的。例如，如果一辆汽车的速度表在一个指定的时间间隔内总是显示一个等于或大于零的数，那么在这个时间间隔内，汽车要么静止不动，要么向前行驶。从几何角度来讲，这条定理说的是，如果一个连续函数的曲线在给定区间内具有一条水平或向上倾斜的切线，那么该函数在这一区间上的值要么不变，要么递增。但是，这种改变也没有流行起来。

许多改革者希望用微积分来解概率论、统计学、生物学和社会科学的实际题目，以取代传统教科书中人为编造的题目。不幸的是，对于尚未在这些领域工作的初学者来说，这些“实际”的题目看起来可能就像那些人为编造的题目一样枯燥而令人生厌。

更激进的改革者认为，高中不应该再开设微积分课程，甚至大学新生也不应该再学习微积分，除非他们已经决定今后要从事一种需要微积分知识的职业。此外，也有反对改革的人，他们认为微积分的传统教学方式不存在任何问题，而前提是当然由称职的教师来教授这门课程。

1992年2月28日，《科学》（Science）杂志调查了杜克大学开设的CALC课程，这是一门面向计算机的微积分课程。只有57%的学生继续学习第二门微积分课程，而作为对比，在学习了更传统的微积分课程后，有68%的学生继续学习高级微积分课程。一些学生喜欢CALC这门试验性的课程，但大多数人并不喜欢。一名学生称这门微积分课程为“我上过的最糟糕的课”，另一名学生则称这是“一场杂乱的大演习”。《科学》杂志还引用了一名学生的话：“我很羡慕我的那些上普通微积分课的朋友。我本该尽力去上一门用纸和笔就能学习的普通微积分课。”

目前的努力是，将连续数学与离散数学结合在同一本教科书中。一个重要的例子是《具体数学：计算机科学基础》（Concrete Mathematics:A Foundation for Computer Science,1984年出版，1989年修订）。这是罗纳德·格雷厄姆、高德纳·克努特和奥伦·帕塔什尼克合著的一本有趣的教科书。这三位作者从“continuous”（连续）的前面取“con”，从“discrete”（离散）的后面取“crete”，构成了“concrete”（具体）一词。不过，即使这本令人兴奋的教科书也预设了读者应具有微积分知识。

1893年，美国哲学家和心理学家威廉·詹姆斯在给日内瓦心理学家西奥多·弗卢努瓦的一封信中问道：“你能否向我推荐一本关于微分学的简单图书，让我深入了解这门学科的基本原理？”

尽管目前微积分的新教学方式纷繁芜杂，但据我所知，没有一本书能像现在你手里拿的这本书那样满足詹姆斯的要求。人们还做出了许多类似的努力，相关的图书有《实用主义者的微积分》（Calculus for the Practical Man）、《微积分入门》（The ABC of Calculus）、《微积分是关于什么的？》（What Is Calculus About?）、《用简易方法学会微积分》（Calculus the Easy Way）和《简化微积分》（Simplified Calculus）等。它们要么过于初级，要么过于高级。汤普森的书正好处于恰当的中间水平。诚然，他的书是老式的、直观的和传统导向的，然而没有一位作者把微积分写得比他更清晰、妙趣横生。汤普森不仅解释了“这门学科的基本原理”，还能教会读者如何对简单函数求微分和积分。

西尔维纳斯·菲利普斯·汤普森出生于1851年，他的父亲是英国约克郡的一所中学的教师。从1885年开始到1916年去世，他一直是芬斯伯里的城市和行会技术学院的物理学教授。作为一名杰出的电气工程师，他于1891年入选英国皇家学会，并担任过多个科学学会的主席。

汤普森写了许多关于电、磁、发电机和光学的专著，其中不少先后出版了好几个版本。他还为科学家迈克尔·法拉第、菲利普·赖斯和开尔文勋爵[3]撰写了广受欢迎的传记。他的讲演很受欢迎，据说他还是一名技艺高超的风景画家。此外，他还写诗。1920年，他的四个女儿中的两个——简·斯米尔·汤普森和海伦·G．汤普森出版了一本关于她们的父亲的书，书名为《西尔维纳斯·菲利普斯·汤普森的生平和信件》（Silvanus Phillips Thompson: His Life and Letters）。

《轻轻松松学会微积分》最早由麦克米伦出版公司于1910年在英国出版。汤普森当时用的是笔名F. R. S.——这是Fellow of the Royal Society（皇家学会会员）的首字母缩写。该书作者的身份直到他去世后才被披露。这本书在1910年底之前就加印了三次。汤普森在1914年对这本书做了大量修改，修正了差错，并增加了一些新的材料。在他去世后，F. G. W．布朗于1919年对这本书做了进一步的修订和扩充，并于1945年再次进行修订和扩充。其中一些后来增加的内容（如关于部分分式和反函数的那一章）比汤普森原著中的那些章节更具技术性。奇怪的是，汤普森的第1版非常简单明了，在某种程度上更接近改革者如今推荐的那种入门书。他们希望强调微积分的基本思想，淡化当今可以用计算机快速解决的烦琐技巧。只想掌握微积分要领的读者可以跳过那些技术性较强的章节，也不必费力解答所有的练习题。这本书从未绝版，圣马丁出版社于1970年出版了平装本。

人们对这本书第1版的评论几乎都是好评。《神殿》（The Athenaeum）杂志的一位评论家写道：

数学文献的评论家很少有运气读到像这样欢快且充满活力的书，“这是对通常有着微分学和积分学这样可怕的名字的那些美丽的计算方法最简单易懂的介绍”。事实上，专业数学家也会热烈欢迎这本书，其教学内容如此正统，阐述如此有力。

汤普森的同事E. G．科克尔教授在写给他的一封信中说：

听说你的那本关于微积分的小书很可能会被广泛使用，我很高兴。正如你所知，我在这里的初级班教授这门学科的基本知识已经有好几年了，我不知道还有哪本书能如此适用于微积分基本思想的教学。这本小书的一大优点是，它消除了专业数学家笼罩在这一学科上的种种谜团。我确信，你的这本小书以其处理微积分基本思想的常识性方式将取得巨大成功。

当今许多杰出的数学家和科学家都是从汤普森的这本书开始学习微积分的。莫里斯·克莱因本人也撰写了一本关于微积分的巨著，但他一直推荐这本书，认为这是给想学习微积分的高中生的一本最好的书。已故经济学家兼统计学家朱利安·西蒙给我寄来了一篇尚未发表的论文，标题为“为什么约翰尼（或许还有你）讨厌数学和统计学”［Why Johnnies (and Maybe You) Hate Math and Statistics］。这篇论文对汤普森的这本书给予了高度赞扬：

我问过的每一位专业数学家都对《轻轻松松学会微积分》嗤之以鼻。就我所知，任何地方开设的任何微积分课程都没有使用这本书。尽管如此，但在它首次出版几乎一个世纪之后，它的平装本依然畅销，即使在大学书店里也是如此。它采用了一种概略的体系来教学，从而非常清楚地阐明了微积分的中心思想——用数学家优雅的极限方法很难理解这一思想。

西蒙稍后问道：

（问题）为什么高中生和大学生不能用汤普森的方法来学习微积分？（回答）汤普森的体系有一个无法弥补的致命缺陷：在世界级数学家的眼中，它是丑陋的，而这些数学家已为数学的教学方式处处制定了标准；普通的大学和高中教师以及他们的学生最终都受制于这种伟大审美趣味的霸权。汤普森只不过放弃了那些以其美丽和优雅吸引数学家的演绎手段。

我之前曾提到《迈向精简而生动的微积分》这本书，其中收录了1986年参加在杜兰大学举办的一次关于如何改进微积分教学的会议的数学家们的论文。大多数作者强烈呼吁减少解题技巧，强调对概念的理解，将微积分与计算器的使用结合起来，并将教科书缩减为更精简、更生动的形式。那么，有史以来最精简、最生动的微积分导论就是汤普森的这本《轻轻松松学会微积分》，但彼得·伦兹是那次会议上唯一有勇气赞扬这本书并将其列为参考书的数学家。

微积分中最重要的概念有两个：一是函数，二是极限。汤普森或多或少地假设他的读者理解这两个概念，因此我在预备知识部分试图更清楚地阐述这两个概念的含义。我增加了导数的简短介绍。另外，在《轻轻松松学会微积分》这本书中，我在自己认为有些有趣的事情可说的地方加入了一些脚注。这些脚注标有我的姓名首字母的缩写M. G. ，以区别于汤普森的脚注（标有他的姓名首字母的缩写S. P. T. ）[4]。

在汤普森谈到英国货币的地方，我都把它们的单位换成了美元和美分。另外，术语已更新。汤普森使用的术语“微分系数”（differential coefficient）已经过时。我把它改成了“导数”（derivative）。“不定积分”（indefinite integral）这个术语现在仍然在使用，但它正在迅速被“反导数”（antiderivative）所取代，所以我将“不定积分”替换成了“反导数”[5]。

汤普森遵循英国人的做法，将小数点的位置提高了，这很容易与表示乘号的点混淆。为了符合美国人的习惯，我把所有这样的点都降低了。汤普森使用了一个现已废弃的符号来表示阶乘，我把它改成了我们熟悉的感叹号。在汤普森使用希腊字母ε的地方，我把它改成了英文字母e。汤普森使用符号logε，我把它换成了ln。最后，在一个篇幅相当长的附录中，我把与微积分相关的各种颇有趣味的题目编在了一起。

我希望自己对《轻轻松松学会微积分》原著的修订和补充能使它更容易理解。这不仅是对高中生和大学生来说的，而且对像威廉·詹姆斯这样渴望了解微积分的年长外行来说也是如此。数学处理的大多是静态对象，如圆、三角形和数字。但“外面”的宏大宇宙不是由我们创造的，它处于一种被牛顿称为“流变”的不断变化的状态——每一微秒，它都会神奇地变成另一种不同的状态。

微积分是关于变化的数学。如果你不是数学家和科学家，也不打算成为数学家或科学家，就没有必要掌握手工解答微积分题目的技巧。但是，如果你不去深入了解微积分的本质，不去深入了解詹姆斯所说的微积分的基本原理，就会错过一次伟大的智力冒险。你会错过一个令人振奋的机会，以致于不能一窥由我们头脑中那些神秘的小计算机所创造的最奇妙、最有用的东西之一。

我要感谢迪安·希克森、奥利弗·塞尔弗里奇和彼得·伦兹，他们审阅了这本书的手稿，并提供了大量宝贵的建议和修改意见。

[2].理查德·库朗（1888—1972），德裔美籍数学家，著有多部有影响的经典数学教材。——译者

[3].开尔文勋爵，原名威廉·汤姆森（1824—1907），英国物理学家、工程师，热力学温标（绝对温标）的发明人，被称为热力学之父。他因为在横跨大西洋的电报工程中所做出的贡献而得到维多利亚女王授予的爵位。——译者

[5].由于中文教科书中较常使用“不定积分”，因此在下文中仍将“反导数”译为“不定积分”。——译者

预备知识

1.什么是函数

在数学中，尤其是在微积分中，没有任何其他概念比函数这个概念更基本。1673年，德国数学家和哲学家戈特弗里德·威廉·莱布尼茨（他独立于艾萨克·牛顿发明了微积分）在一封信中首次使用了这个词。从那时起，这个词的含义逐渐得到扩展。

在传统微积分中，函数被定义为两个变量之间的一种关系，它们之所以称为变量是因为它们的值是变化的。假设x和y为变量，如果x的每个值恰好都与y的一个值相关联，那么我们就说y是x的函数。习惯上，用x表示自变量（independent variable），用y表示因变量（dependent variable），因为y的值取决于x的值。

正如汤普森在第3章中所说明的那样，排在英文字母表最后的几个字母传统上用来表示变量，而英文字母表中的其他字母（通常是前几个字母，如a,b, c,…）用来表示常数。常数是方程中具有固定值的那些量。例如，在y=ax+b中，变量是x和y，而a和b是常数。如果y=2x+7，则常数为2和7。当x和y变化时，它们保持不变。

几何函数的一个简单例子是正方形的面积与边长的相关性。在这种情况下，函数称为一对一函数，因为它们之间的依赖关系是双向的。正方形的边长也是面积的函数。

正方形的面积等于边长乘以边长。要将正方形的面积表示为边长的函数，可设y为面积，x为边长，于是就可以写出y=x2。当然，假设x和y是正的。

正方形的边长与对角线之间的关系是一对一函数的一个稍微复杂一点的例子。正方形的对角线是一个等腰直角三角形的斜边。根据毕达哥拉斯定理[1]，直角三角形斜边的平方等于两条直角边的平方和。在这种情况下，两条直角边是相等的。要将正方形的对角线表示为其边长的函数，可设y为对角线，x为边长，然后写出

，或者更简单地写成

。要将边长表示为对角线的函数，可设y为边长，x为对角线，然后写出

，或者更简单地写成

。

最常见的表示函数的方法是将因变量y替换为f (x)，这里的f是“function”（函数）的首字母。因此，y=f (x)=x2就意味着因变量y等于自变量x的平方。比如，对于y=2x-7，我们现在将其改写成y=f (x)=2x-7。这意味着y是x的函数，它的值因表达式2x-7中x的值而定。该表达式的这种形式称为x的显（explicit）函数。如果表达式具有2x-y-7=0这一等价形式，则它称为x的隐（implicit）函数，因为这个等式隐含了它的显函数形式。通过重新排列该等式中的各项，可以很容易地从该式中得出显函数形式。除了f (x)这个符号之外，我们经常也会使用其他符号。

如果我们希望给定y=f (x)=2x-7这个例子中x和y的值，则可以将x替换为任意值，比如6，于是写出y=f (6)=2×6-7，从而得出因变量y的值为5。

如果因变量是单个自变量的函数，那么这个函数就称为一元函数。我们熟悉的例子（都是一对一函数）有：一个圆的周长或面积与半径的关系、一个球的表面积或体积与半径的关系、一个数的对数与该数的关系。

正弦、余弦、正切和正割称为三角函数。对数给出对数函数。指数函数是指自变量x在一个等式中充当指数的函数，如y=2x。当然，还有无数其他已经被命名的更复杂的一元函数。

函数可以依赖多个变量，这就是所谓的多元函数，其中的元数是指自变量的个数。同样，例子不胜枚举。直角三角形的斜边随它的两条直角边而定，这两条直角边不一定相等。（这个函数当然涉及三个变量，但它称为二元函数，因为它有两个自变量。）如果z是斜边，x和y是两条直角边，那么根据毕达哥拉斯定理，我们知道

。注意，这不是一个一对一函数。如果已知x和y，那么z的值就是唯一的，但如果已知z，那么x和y的值并不是唯一的。

二元函数还有另外两个熟悉的例子，其中一个是三角形的面积是其底边和高的函数，另一个是圆柱的表面积是其半径和高的函数，它们都不是一对一函数。

一元函数和二元函数在物理学中无处不在。摆锤的周期是摆长的函数。落石所经过的距离和速度都是下落时间的（一元）函数。大气压是海拔高度的（一元）函数。子弹的动能是一个取决于其质量和速度的二元函数。导线的电阻是一个取决于其长度和圆形横截面直径的二元函数。

函数可以有任意多个自变量。三元函数的一个简单例子是长方体形状的房间的容积，它取决于房间的长、宽和高。四维超长方形的超体积是一个四元函数。

初学微积分的学生必须熟悉如何用笛卡儿坐标系中的一条曲线为一个具有两个变量的等式建立模型。（这个坐标系是以发明它的法国数学家、哲学家勒内·笛卡儿的姓氏命名的。）自变量的值用水平的x轴上的点表示，因变量的值用竖直的y轴上的点表示。平面上的点表示x和y构成的有序数对。如果一个函数是线性的，即它的形式为y=ax+b，那么表示这些有序数对的图像就是一条直线。如果函数不具有y=ax+b形式，那么它的图像就不是一条直线。

图Ⅰ是y=x2在笛卡儿坐标系中的图像，它是一条抛物线。每条坐标轴上的点表示实数（有理数和无理数）,x轴为右正左负，y轴为上正下负。坐标系的原点（两条坐标轴相交的位置）给出有序数对(0,0)。如果x是一个正方形的边长，那么我们假设它既不是零也不是负数，因此相关的曲线就只是该抛物线的右半边。假设这个正方形的边长为3，有一个点从x轴上的3所对应的位置竖直向上移动到该曲线上，然后水平向左移动到y轴上，你就会发现3的平方是9。（我向读者致歉，因为这些都是老掉牙的知识。）

如果一个函数涉及三个自变量[2]，那么它在坐标系中的图像就必须扩展到一个具有x轴、y轴和z轴的三维空间中。我曾经听说过一位教授（我已经不记得他的名字了）喜欢用一种夸张的方式向学生展示这个空间，他一边沿左右方向来回奔跑一边大喊“这是x轴”，然后一边在中间的过道上沿前后方向来回奔跑一边大喊“这是y轴”，最后一边向上跳跃一边大喊“这是z轴”。具有三个以上变量的函数需要一个具有三条以上坐标轴的笛卡儿坐标系。不幸的是，这位教授不能通过奔跑和跳跃来夸张地展示超过三维的坐标系。

注意图Ⅰ中标注的“定义域”（domain）和“值域”（range）。近几十年来，使函数的定义一般化已经成为一种时尚。自变量的取值范围称为函数的定义域，因变量的取值范围称为函数的值域。在笛卡儿坐标系中，定义域由横轴（x轴）上的数组成，值域由纵轴（y轴）上的数组成。

定义域和值域可以是无限集，比如实数集或整数集；或者其中任意一个可以是有限集，比如实数的一部分。例如，温度计上的数表示实数的一个有限区间。如果用温度计测量水温，那么相应的读数位于水结冰的温度和沸腾的温度之间的那个区间。在这里，水银柱的高度相对于水温是一个单自变量的一对一函数。

在现代集合论中，我们不是用方程，而是用一组规则来描述函数。定义函数的这种方法可以推广到完全任意的数集。指定这些规则的最简单的方法是用一张一览表来表示。例如，在图Ⅱ中，左边的8个数构成了某函数的定义域，而与其对应的右边的4个数构成了值域，支配此函数的规则由箭头表示。这些箭头表明了定义域中的每个数都与值域中的单个数相对应。正如你所看到的，左边的多个数可以指向右边的同一个数，反之则不然。这种函数的另一个例子及其图像如图Ⅲ所示，它的定义域由平面上的6个孤立点组成。

因为左边的每个数都恰好指向右边的一个数，所以我们可以说右边的这些数是左边的这些数的函数。可以将右边的这些数称为左边的这些数的“像”。这些箭头称为从定义域到值域的一个“映射”。也可以说这些箭头定义了函数的“对应规则”。

对于在微积分中遇到的大多数函数，其定义域由单个实数区间组成。定义域可能是整个x轴，比如函数y=x2所表明的情况；也可能是一个有界的区间，比如y=arcsin x的定义域由所有满足-1≤ x ≤1的x值组成；还可能在一侧有界，而在另一侧无界，比如

的定义域包含了所有满足x≥0的x值。如果可以在不从纸上提起笔的情况下画出函数的图像，那么我们将这样的函数称为“连续的”，否则就称其为“不连续的”。（对于具有更复杂的定义域的函数，连续性的完整定义也是完全适用的，但这超出了本书的范围。）

例如，刚才提到的三个函数都是连续的。图Ⅳ给出了一个不连续函数的例子，它的定义域由所有实数组成，但它的图像由无穷多段彼此不相连的部分构成。在本书中，我们将几乎只关注连续函数。

注意，如果垂直于x轴的一条直线多次与一条曲线相交，那么这条曲线就不能表示一个函数，因为它将x轴上的一个数映射到y轴上的多个数。图Ⅴ中的曲线显然不是一个函数的图像，因为垂直于x轴的虚线与它相交于三个点。（应该注意的是，汤普森并没有使用“函数”这一现代定义。例如，第11章的图30中的曲线未能通过这样的检验，但汤普森仍认为它是一个函数的图像。）

在函数的这种一般化的定义中，一个一元函数就是任意有序数对的一个集合，它使一个集合中的每一个数x都恰好与另一个集合中的一个数y配对。换言之，在这些有序数对中，x的取值不能重复，但y的取值可以重复。

从这个广义的角度来看待函数，保险箱的组合密码或打开一扇门所需按下的按钮序列都是自然数的函数。要打开一个保险箱，必须把旋钮来回转动到一组随机整数。比如，如果保险箱的组合密码是2-19-3-2-19，那么这些数就是1,2,3,4,5的一个函数。它们代表为了打开保险箱必须按顺序输入的数。类似地，一把开启弹子锁的钥匙上的那些小小的“峰”的高度是这把钥匙长度方向上的位置的一个函数。

近年来，数学家进一步拓宽了函数的概念，使其包括了那些非数的东西。事实上，它们完全可以是任何东西，只要这些东西是一个集合中的元素。函数只不过是一个集合中的每个元素与另一个集合中的一个元素的相关性。这导致“函数”这个词产生了各种各样看起来很荒谬的用法。如果史密斯的头发是红色的，琼斯的头发是黑色的，而鲁宾逊的头发是白色的，那么头发的颜色就是这三个人的函数。各个城镇在地图上的位置是它们在地球上的位置的函数。在一个正常的家庭中，脚趾的总数是家庭成员数的函数。不同的人可以有同一个母亲，但没有一个人会有一个以上的母亲，这使得人们可以说母亲是人的一个函数。正如一位数学家最近所说的，函数已经被推广到了“上天入地”的程度。

有一种方法可以帮助我们理解以这种一般化的方式定义的函数，那就是想象一个有输入口和输出口的黑匣子。一个定义域中的任何元素，无论它是数还是其他东西，都会被放入这个黑匣子。输出口将出现值域中的单个元素。这个黑匣子里的机械装置通过使用控制函数的任何对应规则，神奇地提供了相关性。在微积分中，输入和输出几乎总是实数，而黑匣子中的机械装置则根据等式提供的规则运行。

由于函数的这种一般化的定义会导致一些怪诞的极端情况，现今的许多教育工作者，尤其是那些具有工程背景的教育工作者，都认为向初学微积分的学生介绍如此宽泛的函数定义既会造成困惑，也没有必要。然而，越来越多的现代微积分教科书在用大量篇幅介绍这种一般化的定义。这些教科书的作者认为，将函数定义为从一个任意集合到另一个任意集合的映射是一个强大的、统一的概念，应该教给所有学习微积分的学生。

反对这种做法的那些人则认为微积分不应该涉及脚趾、城镇和母亲。它的定义域和值域应该一如既往地局限于实数，而其函数描述了连续的变化。

一个值得庆幸而令人惊讶的事实是，变幻莫测的奇妙宇宙的各条基本定律都建立在一些相对简单的方程之上。如果不是这样的话，我们对宇宙运作方式的了解肯定会比现在少，牛顿和莱布尼茨可能永远不会发明（或发现？）微积分。

2.什么是极限

即使没有牢牢把握极限的含义，也是有可能理解微积分的，尽管这很困难。作为微分学基本概念的导数就是一个极限，作为积分学基本概念的积分也是一个极限。

为了解释极限的含义，我们在本章中只关注离散变量函数的极限，因为极限从离散的角度更容易理解。当阅读这本书后面的内容时，你会学到如何将极限概念应用于连续变量函数。这些函数被如此命名是因为它们的变量具有连续变化的实数值。离散变量函数中的变量则是从一个值跳到另一个值。还有复变量函数，其变量的取值是复数——基于-1的纯虚平方根的数。汤普森的这本书不讨论复变量函数。

数列是一组按一定顺序排列的数。这些数不必互不相同，也不必是整数。下面考虑数列1,2,3,4,…，这个数列里只有正整数。它是一个无穷数列，因为它可以一直继续下去。如果它停止了，那么它就是一个有限数列。

如果将一个数列的各相邻项用加号连接起来，那么我们就得到了一个级数。若此数列是有限的，则该级数（和式）就给出了一个有限的和；若此数列是无限的，则相加到指定项就会得到一个“部分和”。如果一个无穷级数的部分和随着项数的增加越来越接近一个数k，那么k就称为该级数的部分和的极限，或者称为该无穷级数的极限。此时，我们称该级数“收敛”到k。如果一个级数不收敛，那么我们就说这个级数是“发散的”。

一个无穷级数的极限有时称为它“趋于无穷时的和”，但这当然不是在项数有限的情况下通常算术意义上的和。你无法通过相加获得一个无穷级数的“和”，因为要相加的项数是无限的。当我们谈到一个无穷级数的“和”时，这只是在用一种简捷的方法来命名其极限。

无穷级数可以通过以下三种不同的方式收敛到其极限。

（1）部分和越来越接近极限而没有实际达到极限，但它们绝不会超过极限。

（2）部分和达到极限。

（3）部分和在收敛之前超过了极限。

让我们举几个例子来看看第一种和第三种方式。

公元前5世纪，古希腊哲学家爱利亚的芝诺[3]提出了几个著名的悖论，旨在表明运动中存在着某种极其神秘的东西。其中一个悖论是想象有一位跑者从点A跑到点B。他先跑完全程的一半，然后跑完剩余距离的一半，再跑完剩余距离的一半，以此类推。他每次跑的距离越来越短，跑过的总距离构成了一个减半级数

。随着他与点A之间的距离所构成的级数收敛到1，他与点B之间的距离则趋于其极限零。当然，这位跑者可以用一个沿着从点A到点B做直线运动的点来模拟。这位跑者会到达目的地B吗？

这取决于具体情况。

假设这位跑者在跑完这个级数中的每一项对应的距离之后都会停下来休息一秒。这种情况可以用一枚棋子（代表一个点）来模拟：设想将它从桌子的一边推到相对的一边。你先将棋子推到一半距离处，然后停顿一秒，再将它推到剩余距离的一半处，再停顿一秒。如果这个过程继续下去，这枚棋子（这个点）将越来越接近极限位置，但永远不会到达极限位置。

有一个基于此的老笑话。一位数学教授让一名男生待在一个空房间的一边，让一名漂亮的女生待在对面的墙边。男生得到命令后，向女生走了一半的距离，等了一秒，然后又走了剩余距离的一半，以此类推。他每次在把剩下的距离减半之前总会停顿一秒。女生说：“哈哈，你永远也到不了我这里！”男生回答道：“没错，但我可以足够接近你。”

现在假设在每一次推动棋子后不再等待一秒，而是以稳定的速度移动这枚棋子。再假设这个恒定速度能使这枚棋子在一秒内走全程的一半，在半秒内走完此时剩余距离的一半，以此类推，在这个过程中没有任何停顿。这样，一个离散的过程就转变成了一个连续的过程。两秒后，棋子就到达了桌子的另一边。如果芝诺所说的跑者以某一速度前进，那么他就会在一段有限的时间后到达目的地。以这种方式建模所构成的减半级数恰好收敛于这一极限。

芝诺所说的跑者引出了各种有趣的悖论，它们涉及所谓的“无限机器”。一个简单的例子是：一盏灯在一分钟后关闭，然后在半分钟后打开，在四分之一分钟后又关闭，以此类推，打开和关闭的时间构成一个无穷级数。这个时间级数收敛于两分钟。两分钟后，这盏灯是开着的还是关着的？这当然是一个思想实验，不能真的用一盏灯来操作，但可以用抽象的方式来回答吗？不行，因为在这个由打开和关闭的时间构成的无穷级数[4]中，不存在最后一次运算。这就好像在问π的最后一位数是奇数还是偶数。

要想“看到”

的极限是1，有一种简单的方法是像汤普森在第17章的图46中所做的那样，沿着一条数轴标出这些分数对应的长度。图Ⅵ中的这个被剖分的单位正方形展示了一种类似的“看了就明白”的证明，我们由此可以看出该级数收敛到1。这个级数的部分和由离散变量函数

生成[5]，其中n取整数1,2,3,4,5,…。

我们现在看一个在最终收敛之前超过了其极限的无穷级数。将刚才那个减半数列中每间隔一项的加号改为减号，就给出了这样的一个例子：

。这个“交错级数”（alternating series）的部分和交错地大于和小于

这一极限，它们与

之差可以任意小，但每一个结束于正项的部分和都大于该极限。

当一个无穷级数逼近而永远不会达到其极限时，部分和与极限之差越来越接近零。事实上，它们如此接近，以至于你可以假设它们的差就是零。因此，正如汤普森喜欢说的那样，它们的差可以被“扔掉”。在早期的微积分书籍中，无限接近零的那些项就称为“无穷小”。这些数生活在无限接近零而不知何故又不是零的梦幻之地，它们显然有些令人毛骨悚然。例如，在那个减半级数中，那些接近零的分数永远不会变成无穷小，因为它们始终是1的一个有限部分。无穷小是1的一个无穷小部分。它比你能说出的任何有限分数都要小，但永远不会为零。它是合法的数学实体吗？应该将它从数学中驱逐出去吗？

最直率地反对无穷小的是18世纪的英国哲学家乔治·伯克利主教。他在1734年出版了一本名为《致异教徒数学家或分析家》（The Analyst, or a Dis‐course Addressed to an Infidel Mathematician）的书，在其中抨击了无穷小。那位异教徒数学家就是天文学家埃德蒙·哈雷，哈雷彗星就是以他的姓氏命名的，他还说服牛顿出版了著名的《自然哲学的数学原理》（The Principia:Mathematical Principles of Natural Philosophy）。

以下是伯克利主教对无穷小的一些抱怨。（“流数”是牛顿用来表示导数的一个术语。）

这些流数是什么？是倏逝增量的速度。这些同样的倏逝增量又是什么？它们既不是有限的量，也不是无穷小的量，但也不是无。我们能不能将它们称为已逝的量的鬼魂呢？

除了上述流数外，还有其他流数，这些流数的流数称为二阶流数。而这些二阶流数的流数则称为三阶流数，以此类推，接下去还有四阶流数、五阶流数、六阶流数等，直至无穷。正如我们的感官对于那些极其微小的物体的感知十分吃力和困惑，要依靠源自感知的想象力去构建关于时间的极小量或其中产生的最小增量的清晰想法也让人感到十分吃力和困惑。更困难的是要理解瞬间，或那些处于刚开始存在的状态的流动量的增量：在它们最初起源或开始存在之后，成为有限的极小量之前。而要想象从这种新生的不完美实体中分离出来的速度，似乎就愈加困难了。但速度的速度，二阶速度、三阶速度、四阶速度和五阶速度等，如果我说得没错的话，这些都超过了所有人的理解能力。大脑越去分析和追求这些难以捉摸的想法，就越会感到迷茫和困惑。这些事物起初转瞬即逝、细微异常，很快就消失在视线之外。无疑，在任何意义上，二阶流数或三阶流数看起来都是晦涩难懂的谜。一个刚出现的速度的刚出现的速度，一个刚开始存在的增长的刚开始存在的增长，是一个没有大小的东西。不管从什么角度看，如果我没说错的话，人们会发现对它是不可能有清晰概念的。不管是不是这样，我恳求每一位有思想的读者来尝试一下。如果二阶流数是不可想象的，那么我们该怎么看待三阶流数、四阶流数、五阶流数等呢？没有尽头。

依我看来，能够理解二阶流数或三阶流数、二阶差或三阶差的人，在理解或对付神学中的论题时是不会有任何困难或异议的。

瑞士数学家约翰·伯努利[6]在发展微积分方面做出了开创性的工作，他清晰地表达了无穷小的悖论。他说，它们是如此微小，以至于“如果一个量增加（或减少）了一个无穷小，那么这个量没有增大（或减小）”。

在两个世纪的时间里，大多数数学家同意伯克利主教的观点，拒绝使用“无穷小”这个术语。你不会在《轻轻松松学会微积分》这本书中找到它。伯特兰·罗素[7]在1903年出版的《数学原理》（Principles of Mathematics）一书的第39章和第40章中对无穷小进行了有力的抨击。他称它“在数学上是无用的”“不必要的、错误的和自相矛盾的”。迟至1941年，著名数学家理查德·库朗写道：“这些无穷小的量现在被明确地、不光彩地抛弃了。”和罗素等人一样，他认为微积分应该用极限的概念来取代无穷小。

威廉·詹姆斯[8]的朋友、美国伟大的数学家和哲学家查尔斯·皮尔斯[9]对此表示强烈反对。当时，他几乎是唯一支持莱布尼茨的人。莱布尼茨认为无穷小和虚数一样真实合理。以下是皮尔斯的一些典型评论。我在皮尔斯撰写的《论文集》（Collected Papers）和《数学新元素》（New Elements of Mathematics）的各卷本的索引中查找“无穷小”时，发现了这些评论。

无穷小可能存在，并且对哲学非常重要，正如我所相信的那样。

慷慨地承认虚数，同时又将无穷小视为不能想象而加以抵制……这是自洽的吗？

从严格意义和字面意义上讲，无穷小是完全可以理解的，这与大量现代微积分教科书中的说法相反。

关于这样的一些量的想法并没有任何矛盾之处……作为一名数学家，我更喜欢无穷小的方法，而不是极限的方法，因为前者理解起来要容易得多，而且更少受到各种陷阱的滋扰。

如果皮尔斯生前能看到耶鲁大学的亚伯拉罕·鲁宾逊[10]的研究，他一定会感到很高兴。1960年，令世界各地的数学家感到惊讶的是，鲁宾逊找到了一种方法，将莱布尼茨的无穷小作为合法的、精确定义的数学实体重新引入！他在微积分中使用无穷小的这种方法称为“非标准分析”。（“分析”是一个应用于微积分和所有要用到微积分的高等数学的术语。）对于许多微积分问题，非标准分析给出了比标准分析更简单的解答，它无疑更接近一种解释无穷收敛级数的直观方法。鲁宾逊的成就很难在这里详细介绍，但你能在马丁·戴维斯和鲁本·赫什的《非标准分析》（Nonstandard Analysis）中找到很好的介绍。此文发表在1972年6月的《科学美国人》（Scientific American）上。

数学家和科幻作家鲁迪·鲁克在其著作《无穷与心灵》（Infinity and the Mind,1982年）中极力捍卫无穷小：

普通人对于无穷是如此恐惧，以至于直到今天，全世界教授微积分的人都是将其作为对极限过程的研究，而不是在其真正含义——无穷小分析上进行研究。

作为一个成年后大部分时间以教授微积分课程为生的人，我可以告诉你，试图向一届又一届不理解复杂而又烦琐的极限理论的新生解释这些理论，这是多么令人感到厌倦……

但更为光明的未来还是有希望的。鲁宾逊对超实数的研究将无穷小建立在一个逻辑上无懈可击的基础之上，而基于无穷小的微积分教科书也在各地出现了。

哪一种方式更可取？是去谈论那些无穷小的量，这些量如此之小，以至于如汤普森所说，你可以“把它们扔掉”，还是去谈论那些接近某个极限的值？关于无穷小与极限这种语言之间的争论毫无意义，因为它们只是同一事物的两种说法。这就像是将三角形称为有三条边的多边形，还是称为有三个角的多边形。微分或积分的计算是完全一样的，这与你喜欢如何去描述你在做的事情无关。现在，由于有了非标准分析，无穷小又变得体面了，你只要愿意就可以毫不犹豫地使用这个术语。

你可能会认为，如果一个无穷级数的项变得越来越小，那么这个级数必定是收敛的。但是，事实绝非如此。最著名的例子是

。这个级数称为“调和级数”，它在物理学和数学中都有着无数的应用。尽管其中的分数变得越来越小，逐渐收敛到零，但它的部分和在无限增大，没有极限！这个级数的部分和的增长速度慢得令人恼火：在100项之后，它的部分和仅比5略大一点；要到1045项之后，它的部分和才能达到100！

如果我们在这个调和级数中去掉所有分母为偶数的项，它会收敛吗？令人惊讶的是，它也不收敛，尽管它的增长速度更慢。如果我们从这个级数中去掉分母中一次或多次包含某一特定数字的所有项，那么这个级数就会收敛了。对于每个被去掉的数字，表Ⅰ给出了该级数精确到小数点后两位的极限。

无穷级数的极限可以用无限小数来表示。例如，0.333333…是级数

的极限。顺便说一下，有一种简单得不可思议的方法可以确定任何循环小数的整分数极限。这里的诀窍是：循环节（重复数字段）由几位数字构成，就将循环节除以几个9[11]。因此，0.3333…就简化成

。如果循环小数是0.123123123…，那么它的极限就是

，这个分数可化简为

。

无理数，比如无理根以及像π和e这样的超越数[12]，是许多无穷级数的极限。例如，π是像

这样高度有规律的级数的极限，数字e[13]（你会在本书的第14章中遇到它）是

的极限。

虽然阿基米德并不知道微积分，但他计算圆周率的方法是将正多边形的周长随着其边数增加的极限作为圆的周长，这就已经蕴含了积分的思想。我们可以用无穷小的语言来这样表述：一个圆可以被视为一个具有无穷多条边的正多边形，其周长由无穷多条线段组成，每条线段的长度都是无穷小。

人们已经发现了许多技巧来判定一个无穷级数是收敛的还是发散的，还发现了一些在收敛时求出极限的方法，有时这些方法用起来并不容易。如果一个等比级数（每相邻两项之比不变）中的各项在减小，那么我们就很容易求出其极限。以下是求减半级数

的极限的方法。设x等于整个级数，即

。在该等式的两边都乘以2，有

约化各项，可得

注意，1之后的这个级数与我们取为x的原始减半级数相同。这样，我们就能用x来替换该级数，从而将上式写成2x=1+x。重新整理各项，有2x-x=1，由此得到该级数的极限x的值为1。

利用同样的技巧可以求出

是

的极限。这种方法适用于各项递减的任何等比级数。

在有关极限的文献中，关于弹跳球的题目很常见。这些题目假设一个理想的弹跳球从距离地面一定高度处掉落到坚硬的地板上。每次反弹后，它都会上升到前一次下落高度的一个恒定比例处。下面是一个典型的例子。

弹跳球从4英尺高处掉落，每次反弹后都会达到前一次下落高度的

处。当然，在实际情况下，橡胶球只能反弹有限次，但这个理想化的弹跳球能反弹无限多次。弹跳球反弹的高度逐渐逼近极限零，但由于每次反弹所用的时间也逼近极限零，因此这个弹跳球（就像芝诺所说的跑者一样）最终会到达极限位置。经过无限多次反弹之后，它会在一段有限的时间后停下来。在这个弹跳球停止反弹前，它所经过的距离一共是多少？

我们可以再次利用刚才用于计算减半级数极限的那种技巧，暂时只考虑弹跳球最初下落4英尺以后第一次反弹的情况：弹跳球会上升3英尺，然后下落3英尺，这样它经过的距离总共为6英尺。此后每次反弹（上升加下落）的距离都是前一次反弹距离的

。设x为弹跳球第一次下落4英尺以后经过的总距离，我们写出等式：

约化这些分数，可得

由于每一项都是其后一项的

，我们在上式两边同时乘以

，得到

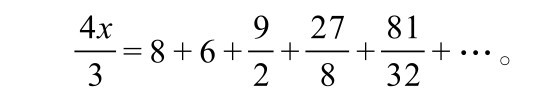
注意，在8之后，这个级数与x是相同的，因此我们可以用x来替换它，则有

这是弹跳球在最初下落4英尺以后多次反弹经过的距离，因此这个弹跳球经过的总距离为24+4=28（英尺）。

美国伟大的益智题设计大师萨姆·劳埃德在他的《世界经典智力游戏》（Cyclopedia of Puzzles）[14]中以及他的英国同行亨利·欧内斯特·杜德尼在《益智题与奇趣题》（Puzzles and Curious Problems）第223题中各自给出了下面这道关于球反弹的题目。一个球从比萨斜塔的179英尺高处下落（见图Ⅶ），每次反弹的高度是上一次下落高度的

。这个球经过无限次反弹，在最终停止之前会经过多长距离？

我们可以利用前面用过的那种技巧来解答此题，但因为每次反弹的高度都是上一次下落高度的

，所以我们可以采用一种更快捷的方法找到答案。

在最初下落179英尺之后，第一次反弹的高度是17.9英尺。随后各次反弹的高度分别为1.79英尺，0.179英尺，0.0179英尺，以此类推。将这些数相加，得到总和为19.8888…英尺。我们现在将这个距离加倍，就得到各次反弹后上升和下落的距离之和为39.7777…英尺。最后，我们加上最初下落的179英尺，就得到这个球经过的总距离为218.7777…英尺，或者说是

英尺。

对于不按等比级数方式递减的收敛级数，常常可以利用另外一些巧妙的方法来求其极限。下面有一个有趣的例子：

注意，此级数中各分数的分子构成了一个奇数数列，而分母则构成了一个加倍数列。这里用一种简单的方法来求出它的极限。

首先将每一项都除以2，则有

用原级数减去这个级数，可得

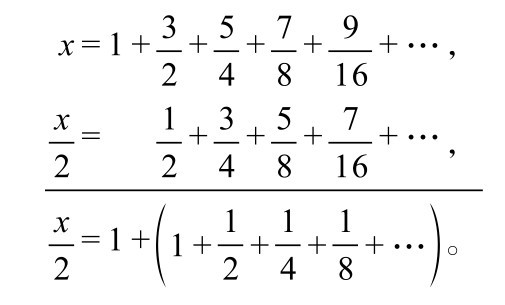
注意，在括号内的1之后，接下去的级数就是我们的老朋友减半级数了，我们知道它收敛于1。用上式中右边的第一个1加上括号里的运算结果2，得到3。由于3是x的一半，x就必定是6，即原级数的极限为6。

汤普森没有花费太多时间讨论级数及其极限。我在这里讨论这些出于两个原因：其一，这是我们适应极限概念的最佳方式；其二，当前的微积分教科书通常都有一些章节论述无穷级数及其在微积分的许多方面的应用。

3.什么是导数

在第3章中，汤普森非常清楚地说明了什么是导数，以及如何计算导数。不过，在我看来，对导数做一些简要的评论会有一定的帮助，这可能会使第3章更容易理解。

让我们从芝诺的跑者开始。假设他在一条100米长的路上以10米/秒的速度奔跑。这里的自变量是时间，用笛卡儿坐标系的x轴表示；因变量是跑者和起点之间的距离，用y轴表示。因为这个函数是线性的，所以跑者的运动图像是一条向上倾斜的直线，从坐标系的原点一直延伸到对应于x轴上的10秒和y轴上的100米的点（见图Ⅷ）。如果我们所说的距离是指跑者和终点之间的距离，那么图Ⅷ中的直线就会向另一个方向倾斜（见图Ⅸ）。

任意给定一个时间点，让我们看看这位跑者此时的速度。因为我们处理的是一个简单的线性函数，所以我们不需要微积分就能知道他每一瞬间都在以10米/秒的速度前进。这个函数的方程为y=10x。注意，这条直线的斜率为10，这是用任一点到起点的距离（以米为单位）除以跑者到达这一点所用的时间（以秒为单位）来度量的。在每一瞬间，跑者经过的米数都是所用秒数的10倍。在整个跑步过程中，他的瞬时速度显然是10米/秒。

考虑x轴上的一个任意点，然后在坐标系中将其竖直向上移动到以米为单位的对应位置，你会发现移动的距离总是所用的时间的10倍（只考虑数值，略去单位）。当阅读这本书时，你会学到函数的导数只不过是另一个函数，它描述的是因变量相对于自变量变化的变化率。在这种情况下，跑者的速度始终保持不变，因此y=10x的导数就是10。它告诉你两件事：（1）在任何时刻，跑者的速度都是10米/秒；（2）这个函数图像上的任何一点的斜率都是10。这两点可以推广到变量y相对于变量x以恒定速率变化的所有线性函数。如果一个函数是y=ax，那么它的导数就是常数a。

正如我说过的，你不需要微积分就能知道这一切，但是对于线性函数，通过计算导数也能得到正确的结果。知道这一点也是很好的。

导数的一个更简单的例子是完全静止的跑者。这个例子太显而易见了，我们不需要任何思考，更不用说使用微积分了。假设跑者跑了10米以后就停了下来，那么此后的情形对应的函数就是y=10。该函数的图像是一条水平直线，如图Ⅹ所示。这条直线的斜率为零，这就相当于说跑者停下来的那个点和起点之间的距离相对于时间的变化率为零。这个函数的导数为零。即使在这种极端情况下，微积分仍然适用也是令人欣慰的。一般而言，任何常数函数的导数都是零。

当函数是非线性的时候，微积分就不再那么不值得一提了。考虑y=x2这个简单的非线性函数，汤普森用它来开始他关于导数的那一章。对这个函数的最简单的几何解释是它表示一个正方形的面积。现在让我们看看它是如何应用于正方形的增大的。

想象有一头怪物生活在平面国[15]，那是一个二维平面。它出生时是一个边长为1、面积也为1的正方形，然后以稳定的速率增大。我们希望知道，在任何时刻，正方形的面积相对于边长增大的速率是多少。

这头怪物的面积当然就是其边长的平方，因此我们必须考虑的函数是y=x2，其中y是面积，x是边长。（它的图像就是前面图Ⅰ中的那条抛物线的一半。）正如你将从汤普森所写的内容中学到的，这个函数的导数是2x。这告诉我们什么？这告诉我们，在任一给定时刻，这头怪物的面积增大的速率都等于其边长增大的速率的2x倍。

假设这头怪物的边长以每秒3个单位的速率增大。它的边长从1个单位开始增大，到10秒末，它的边长会达到31个单位。此时，x的值为31。上面的导数表明，这头怪物的面积相对于边长以2x的速率增大，而当其边长为31个单位时，其面积相对于边长的增量为62个平方单位/单位。当正方形的边长达到100个单位时，其面积相对于边长的增量为200个平方单位/单位。

这些数表示正方形的面积相对于边长的增大率。对于正方形的面积相对于时间的增大率，我们还必须将这些数乘以3。因此，当正方形的边长为31个单位时（10秒后），它的面积会以每秒186个平方单位的速率增大，即3 × 2 × 31=186；当正方形的边长为100个单位时，其面积增大的速率为每秒600个平方单位，即3 × 2 × 100=600。

假设这头怪物是一个棱长为x的立方体，而x以每秒2个单位的稳定速率增大。立方体的体积y等于x3。函数y=x3的导数是3x2。这告诉你，立方体体积（以立方单位为单位）增大的速率是其边长增大的速率的3x2倍。因此，当立方体的棱长x为10个单位时，其体积相对于棱长的增量为300个立方单位/单位，即3 × 102=300。它的体积增大的速率是每秒600个立方单位，即2 × 3 × 102=600。

尽管汤普森避免将导数定义为比值的极限，但情况显然就是这样。举例来说，这个不断增大的正方形的边长以每秒1个单位的速率增大时，我们可以将它的面积在2秒及以后的一系列时刻的增大情况制成表格（见表Ⅱ）。

从2秒到2.1秒的平均增大速率为

从2秒到2.01秒的平均增大速率为

从2秒到2.001秒的平均增大速率为

这些平均值显然在逼近极限6。因此，面积相对于时间的导数就是一个无限的比率数列的极限，该数列收敛于6。简单地说，导数是函数的因变量相对于自变量的增大速率的增大速率。从几何角度来看，它确定了一条函数曲线上任何指定点的切线的精确斜率。导数的代数定义与几何定义之间的等价性是微积分最美妙的方面之一。

我希望这些预备知识能帮助你为学习后面的内容做好准备。

[1].毕达哥拉斯定理，即我们所说的勾股定理，在西方相传由古希腊的毕达哥拉斯首先证明，而在中国相传于商代就由商高发现。——译者

[3].芝诺（约前490—前430），古希腊数学家、哲学家，他提出了一系列关于运动不可分性的哲学悖论。——译者

[4].关于无穷机器，请参阅我的《轮子、生命和其他趣味数学》（Wheels, Life, and Other Mathematical Amuse‐ments,1983年）第4章“א和超任务”（Alephs and Supertasks），以及那一章引用的参考文献。——M.G.

[5].级数

是一个等比级数，其首项

，公比

，因此部分和

。——译者

[6].约翰·伯努利（1667—1748），瑞士数学家、物理学家，在微积分、天体力学、流体力学等方面做出了重要贡献。伯努利家族共产生了11位数学家。——译者

[7].伯特兰·罗素（1872—1970），英国哲学家、数理逻辑学家，1950年诺贝尔文学奖获得者，分析哲学的创始人之一。——译者

[8].威廉·詹姆斯（1842—1910），美国本土第一位哲学家和心理学家，也是教育学家、实用主义的倡导者。——译者

[9].查尔斯·皮尔斯（1839—1914），美国通才，早年为化学家，他在数学、研究方法论、科学哲学、知识论和形而上学领域都进行了改革，并创建了作为符号学分支的逻辑学，也是美国当代实用主义的奠基人。——译者

[10].亚伯拉罕·鲁宾逊（1918—1974），德裔美国数学家，非标准分析的奠基人。——译者

[11].假如讨论的数是k=0.ababab…，那么100k=ab+k，于是有(100-1)k=ab，即

。同理，可讨论其他情况。——译者

[12].参见《从代数基本定理到超越数：一段经典数学的奇幻之旅（第二版）》，冯承天著，华东师范大学出版社，2019年。——译者

[13].参见《优雅的等式：欧拉公式与数学之美》，戴维·斯蒂普著，涂泓、冯承天译，人民邮电出版社， 2018年。——译者

[15].这一典故出自埃德温·A．阿博特的《平面国：一部多维的罗曼史（双语版）》（Flatland:A Romance of Many Dimensions），该书首次出版于1884年，已成为科幻小说的经典之作。此书有多个中译本，近期的双语版由高等教育出版社于2022年出版，涂泓译，冯承天译校。——译者