

书名:高考圆锥曲线探秘:从体系到技巧
ISBN:978-7-115-67236-0
本书由人民邮电出版社发行数字版。版权所有,侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用,未经授权,不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟,与我们共同保护知识产权。
如果购买者有侵权行为,我们可能对该用户实施包括但不限于关闭该帐号等维权措施,并可能追究法律责任。
著 董晟渤 李心睿
责任编辑 李 宁
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
网址 http://www.ptpress.com.cn
读者服务热线:(010)81055410
反盗版热线:(010)81055315
圆锥曲线是高考数学的重难点,近几年常在高考数学试卷的最后一题出现.本书系统介绍圆锥曲线的基本定义和统一定义、有心圆锥曲线的第三定义、参数方程、极线等知识,讲解点差法、联立、齐次化联立、同构式、不联立等常用的计算技巧,适合高中生和高中数学老师阅读.
2024 年《高考导数探秘:解题技巧与策略》一书出版后,我收到了许多读者的好评与反馈.在众多的反馈中,读者问得最多的一个问题是,什么时候再写一本关于圆锥曲线的书?考虑到圆锥曲线也是高考的重难点,我梳理了平时讲授圆锥曲线课程的思路,整理了之前在知乎上创作的文章,与李心睿一起编著了本书.本书的大部分正文内容由我完成,例题、课后练习和不联立的相关内容主要由李心睿完成.
近几年来,圆锥曲线常在高考数学试卷的最后一题出现(如 2023 年新课标Ⅰ卷和 2024年新课标Ⅱ卷),题目越来越灵活.学生在学习圆锥曲线时可能会陷入两个“陷阱”:一个是不断记忆各种二级结论,希望通过二级结论直接“秒杀”题目,而没有建立圆锥曲线的知识体系,忽略了现在高考“反套路”的现实;另一个是沉迷于各种“奇技淫巧”或者计算方法,没有理解技巧和方法背后的原理,知其然而不知其所以然.在我看来,无论学习数学的哪个模块,都应该对知识点、技巧和方法有本质理解,这样才能在考场上见招拆招.
本书只有两章,第1章主要梳理圆锥曲线的知识体系,第2章则对圆锥曲线的计算技巧进行讲解.
第1章展开介绍了圆锥曲线的基本定义和统一定义(也被称为第二定义)、有心圆锥曲线的第三定义与点差法.除了传统的点差法以外,本书还介绍了与定比分点相关的点差法,这是一个常会用到的计算技巧.除了介绍定义以外,本书还在第1章里介绍了常见曲线的参数方程,展开讲解了椭圆的压缩变换.圆锥曲线中还有一个重要的结论是关于极点和极线的,例如对于椭圆 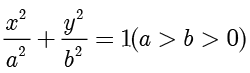 而言,点
而言,点 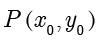 所对应的极线的方程为
所对应的极线的方程为 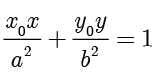 .圆锥曲线的极线和切线密切相关.
.圆锥曲线的极线和切线密切相关.
第2章围绕圆锥曲线中的计算问题展开.在做圆锥曲线的题目时,读者比较熟悉的方法是将直线方程与圆锥曲线方程联立,再使用韦达定理计算 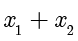 和
和 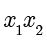 ,进一步计算
,进一步计算 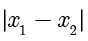 .除了传统的联立方法以外,本书还介绍了齐次化联立的技巧,以及圆雉曲线中的同构式.本书中比较有特色的是介绍了不联立的技巧,这是一种以设点为主的计算技巧,包括使用点差法计算斜率和使用平方差公式求解非对称问题两种思路.最后本书整理了圆锥曲线中常见的模型,这些模型常常作为命题的背景.
.除了传统的联立方法以外,本书还介绍了齐次化联立的技巧,以及圆雉曲线中的同构式.本书中比较有特色的是介绍了不联立的技巧,这是一种以设点为主的计算技巧,包括使用点差法计算斜率和使用平方差公式求解非对称问题两种思路.最后本书整理了圆锥曲线中常见的模型,这些模型常常作为命题的背景.
本书适合数学成绩较好、希望能进一步学习圆锥曲线的高二或高三的学生,同时本书也适合作为正在讲授圆锥曲线的高中数学老师的讲义.对于大多数学生来说,必须要掌握的是本书1.1节中的圆锥曲线的基本定义、1.2节中的焦半径公式与焦点三角形的性质、1.3节中的点差法、2.1节中的直线方程与圆锥曲线方程联立,以及 2.2 节中的长度、面积和角度的计算.本书2.3节和2.4节讲解的都是“非传统方法”,但是自 2.3 节开始的所有例题和练习题都可以使用2.1节和2.2节所介绍的传统方法解答,因此读者不必因为没有学过齐次化联立和不联立的计算技巧而焦虑.不过,对于学有余力的学生而言,本书所有的内容都是适合的.书中带星号(*)的部分是高考不要求掌握的内容,但是这些内容(如参数方程)对于读者建立知识体系有帮助,所以也被收录在本书当中.
回顾编著本书的过程,我首先要感谢李心睿提供的优质题目和为本书付出的努力.除此之外,特别感谢陈宇灿、吴梓帆、熊雄、叶纳诚(按照姓氏拼音排序),他们帮助完成了本书的审校工作,并提供了宝贵的建议.希望读者能够通过本书,梳理清楚圆锥曲线从定义到极点、极线的知识体系,熟悉从传统联立到齐次化联立再到不联立的计算技巧.相信读者一定能有所收获!
董晟渤(Dylaaan)
2025年3月于燕园
圆锥曲线包含椭圆、双曲线和抛物线 3 种曲线,是本书的主要研究对象.在讲解圆锥曲线的题目之前,我们需要先回顾圆锥曲线的定义.本章首先介绍了高中课本上圆锥曲线的基本定义,然后介绍圆锥曲线的统一定义,以及有心圆锥曲线(即椭圆和双曲线)的第三定义.
定义1.1(椭圆) 设 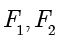 是平面内的两个定点,
是平面内的两个定点,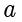 是一个常数,且
是一个常数,且 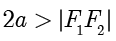 .平面内满足
.平面内满足
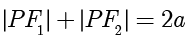
的动点 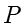 的轨迹称为椭圆.其中,两个定点
的轨迹称为椭圆.其中,两个定点 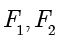 称为椭圆的焦点,两个焦点之间的距离
称为椭圆的焦点,两个焦点之间的距离 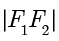 称为椭圆的焦距.特别地,如果
称为椭圆的焦距.特别地,如果 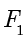 和
和 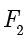 重合,则动点
重合,则动点 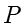 的轨迹是圆.
的轨迹是圆.
研究包含椭圆在内的圆锥曲线需要借助解析几何的方法,也就是说,将曲线放在平面直角坐标系中,使用坐标和方程来研究曲线的性质.那么,椭圆在平面直角坐标系中应该是什么样子的呢?一般来说,我们以 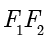 所在直线为
所在直线为 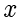 轴,
轴,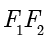 的垂直平分线为
的垂直平分线为 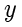 轴,建立平面直角坐标系
轴,建立平面直角坐标系 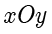 ,如下图所示.设椭圆的焦点分别为
,如下图所示.设椭圆的焦点分别为 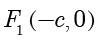 和
和 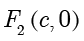 ,并设
,并设 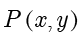 在椭圆上,满足
在椭圆上,满足 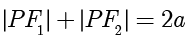 ,下面推导椭圆的方程.
,下面推导椭圆的方程.
平面直角坐标系 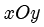 中的椭圆,其中
中的椭圆,其中 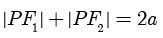
根据点到直线的距离公式,可得
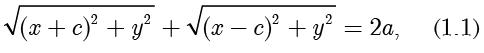
当 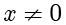 时,
时,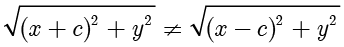 ,对上式左边进行分子有理化,可得
,对上式左边进行分子有理化,可得
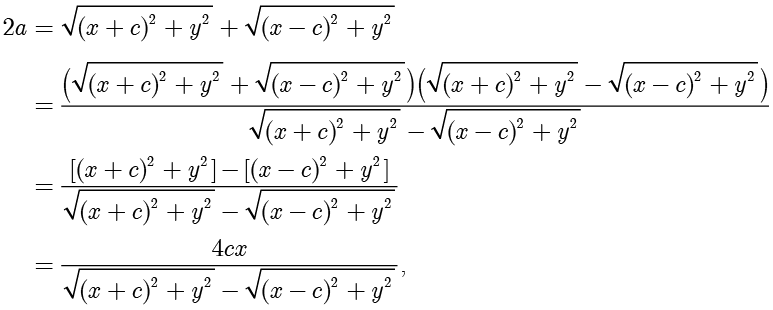
因此
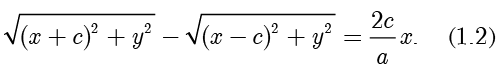
由方程(1.1)和方程(1.2)相加得
[1] 事实上,这里得到了 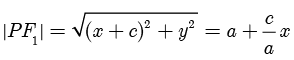 ,若记
,若记 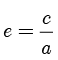 ,则有
,则有 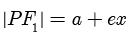 ,同时可以推导得到
,同时可以推导得到 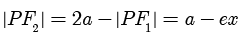 .这个公式称为焦半径公式,借助这个公式可以大大简化计算过程.我们在后面会展开介绍.
.这个公式称为焦半径公式,借助这个公式可以大大简化计算过程.我们在后面会展开介绍.
上式右边是非负的,等式两边同时平方并整理得 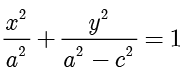 .可以验证当
.可以验证当 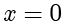 时,方程(1.1)的解满足该方程.一般来说,记
时,方程(1.1)的解满足该方程.一般来说,记 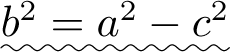 ,即可得到椭圆的标准方程
,即可得到椭圆的标准方程
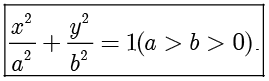
椭圆 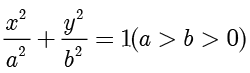 的图像如下图所示.
的图像如下图所示.
椭圆 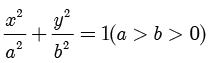 的图像
的图像
考虑椭圆 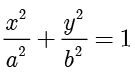 ,其中
,其中 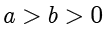 ,
,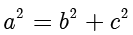 .
.
● 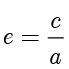 称为椭圆的离心率,且
称为椭圆的离心率,且 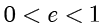 .
.
● 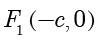 和
和 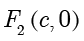 分别称为椭圆的左焦点和右焦点.
分别称为椭圆的左焦点和右焦点.
● 椭圆与 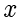 轴的交点为
轴的交点为 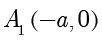 与
与 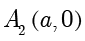 ,与
,与 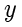 轴的交点为
轴的交点为 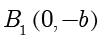 与
与 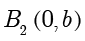 .
. 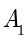 和
和 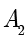 分别称为椭圆的左顶点和右顶点,
分别称为椭圆的左顶点和右顶点,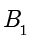 和
和 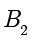 分别称为椭圆的下顶点和上顶点.
分别称为椭圆的下顶点和上顶点.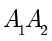 称为椭圆的长轴,
称为椭圆的长轴,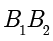 称为椭圆的短轴.
称为椭圆的短轴.
● 对于椭圆上的点 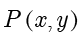 ,有
,有 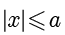 和
和 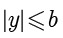 .
.
例题1.1(取自2016年Ⅰ卷理数[2]) 设圆 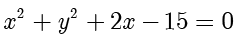 的圆心为
的圆心为 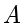 ,直线
,直线 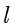 过点
过点 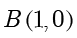 且与
且与 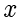 轴不重合,
轴不重合,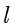 交圆
交圆 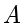 于
于 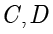 两点,过
两点,过 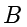 作
作 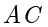 的平行线交
的平行线交 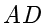 于点
于点 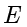 .证明
.证明 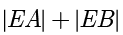 为定值,并写出点
为定值,并写出点 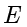 的轨迹方程.
的轨迹方程.
[2] 为了提升阅读体验并简化表达,本书中的高考试卷名称采用了简称形式,例如将“2016 年高考全国Ⅰ卷理科数学”简称为“2016年Ⅰ卷理数”,将“2023 年新课标全国Ⅰ卷数学”简称为“2023 年新课标Ⅰ卷”,以此类推.需特别说明的是, 2025年高考试卷名称在简称规则上有所不同,其名称统一为 2025 年全国一卷和 2025 年全国二卷.这样既保持了信息的真实性,又提高了文本的可读性.此外,本书中的高考试题均来源于公开网络资源,受版本差异影响,个别试题的表述可能存在细微出入.——编者注
满足题意的点 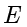 的轨迹如下图所示.
的轨迹如下图所示.
满足题意的点E的轨迹
解答 整理得圆的标准方程为 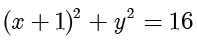 ,因此圆心
,因此圆心 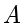 的坐标为
的坐标为 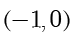 .因为
.因为 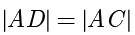 ,
,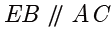 ,所以
,所以 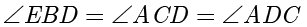 ,所以
,所以 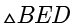 是等腰三角形,故
是等腰三角形,故 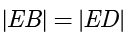 ,计算得
,计算得
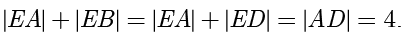
因此 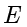 在以
在以 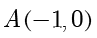 和
和 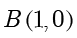 为焦点,以 4 为长轴的椭圆上(不包含与
为焦点,以 4 为长轴的椭圆上(不包含与 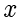 轴的交点),所以点
轴的交点),所以点 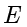 的轨迹方程为
的轨迹方程为 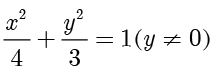 . ■
. ■
例题1.2(取自2023年新课标Ⅰ卷) 设椭圆 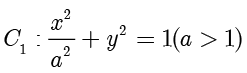 ,
,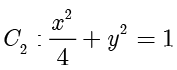 的离心率分别为
的离心率分别为 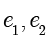 .若
.若 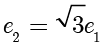 ,则
,则 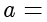 .
.
解答 计算得 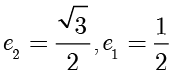 .根据
.根据 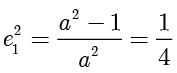 ,解得
,解得 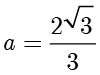 . ■
. ■
例题1.3(取自2025年全国一卷) 设椭圆 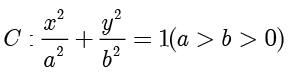 的离心率为
的离心率为 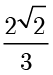 ,下顶点为
,下顶点为 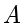 ,右顶点为
,右顶点为 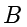 ,
,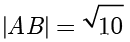 .
.
(1)求  的标准方程;
的标准方程;
(2)已知动点 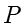 不在
不在 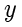 轴上,点
轴上,点 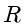 在射线
在射线 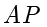 上,且满足
上,且满足 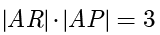 .
.
(i)设 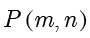 ,求
,求 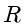 的坐标(用
的坐标(用 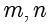 表示);
表示);
(ii)设 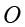 为坐标原点,
为坐标原点,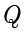 是
是  上的动点,直线
上的动点,直线 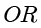 的斜率是直线
的斜率是直线 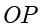 的斜率的 3 倍,求
的斜率的 3 倍,求 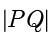 的最大值.
的最大值.
解答 (1)根据题意得 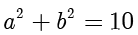 ,
,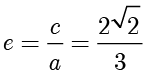 ,结合
,结合 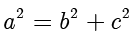 ,解得
,解得 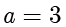 ,
, 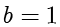 ,
,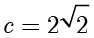 .故椭圆
.故椭圆  的方程为
的方程为 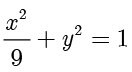 .
.
(2)(i)根据题意得 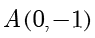 ,
,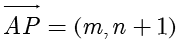 .设
.设 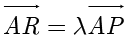 ,代入
,代入 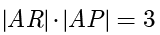 解得
解得 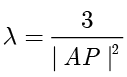 ,因此
,因此
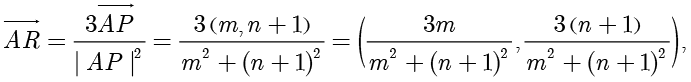
最后得到 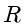 的坐标为
的坐标为 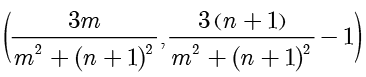 .
.
(ii)设 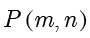 ,首先
,首先 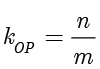 ,由(i)和
,由(i)和 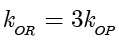 得
得
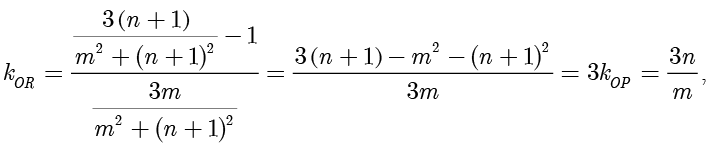
整理得
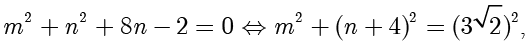
所以点 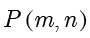 在以
在以 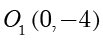 为圆心,半径为
为圆心,半径为 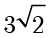 的圆上.设
的圆上.设 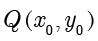 为椭圆
为椭圆  上一点,由三角不等式得
上一点,由三角不等式得
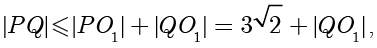
当且仅当 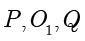 三点共线,且
三点共线,且 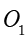 在线段
在线段 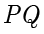 上时取等,因此只需求出
上时取等,因此只需求出 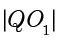 的最大值.根据点
的最大值.根据点 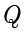 在椭圆
在椭圆  上,可得
上,可得 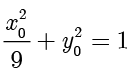 ,因此
,因此
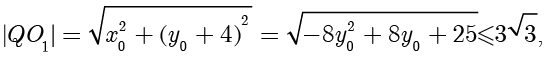
当且仅当 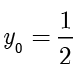 时取等,此时
时取等,此时 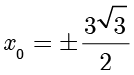 .因此
.因此 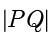 的最大值为
的最大值为 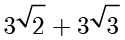 . ■
. ■
在椭圆的定义中将“距离之和”改为“距离之差”,即可得到新的曲线,这个曲线称为双曲线,见如下定义.
定义1.2(双曲线) 设 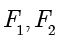 是平面内的两个定点,
是平面内的两个定点,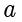 是一个常数,且
是一个常数,且 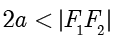 .平面内满足
.平面内满足
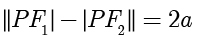
的动点 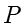 的轨迹称为双曲线.其中,两个定点
的轨迹称为双曲线.其中,两个定点 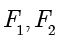 称为双曲线的焦点,两个焦点之间的距离
称为双曲线的焦点,两个焦点之间的距离 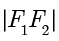 称为双曲线的焦距.
称为双曲线的焦距.
类似随圆的研究方法,我们用解析几何的方法研究双曲线.以 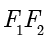 所在直线为
所在直线为 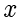 轴,
轴, 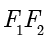 的垂直平分线为
的垂直平分线为 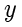 轴,建立平面直角坐标系
轴,建立平面直角坐标系 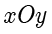 ,如下图所示.设双曲线的焦点分别为
,如下图所示.设双曲线的焦点分别为 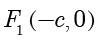 和
和 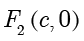 ,并设
,并设 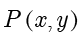 在双曲线上,满足
在双曲线上,满足 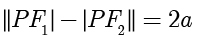 ,下面推导双曲线的方程.
,下面推导双曲线的方程.
平面直角坐标系 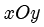 中的双曲线,其中
中的双曲线,其中 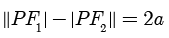
根据点到直线的距离公式,可得
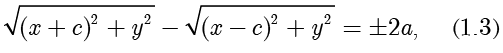
对上式左边进行分子有理化,可得
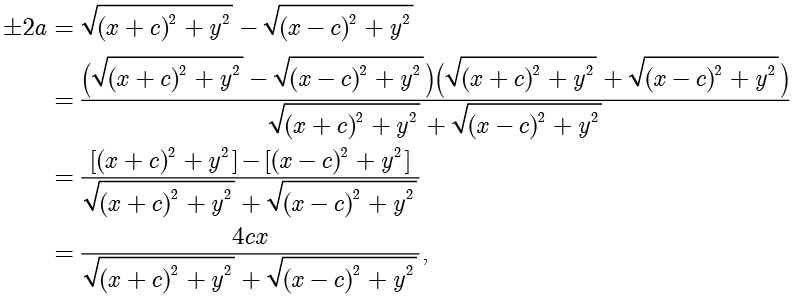
因此
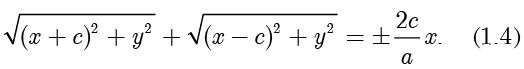
由方程(1.3)和方程(1.4)相加得
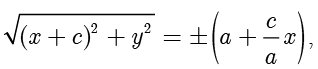
等式两边同时平方,可以验证没有增根,整理得 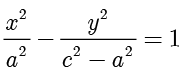 . 一般来说,记
. 一般来说,记 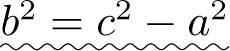 ,即可得到双曲线的标准方程
,即可得到双曲线的标准方程
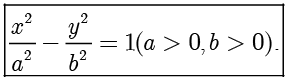
双曲线 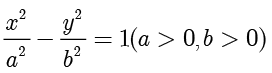 的图像如下图所示.
的图像如下图所示.
双曲线 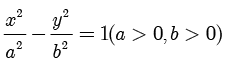 的图像
的图像
考虑双曲线 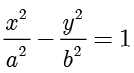 ,其中
,其中 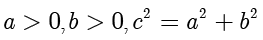 .
.
● 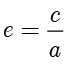 称为双曲线的离心率,且
称为双曲线的离心率,且 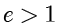 .
.
● 直线 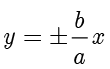 称为双曲线的渐近线[3] .随着
称为双曲线的渐近线[3] .随着 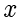 变大或者
变大或者 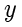 变大,双曲线上的点
变大,双曲线上的点 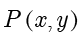 到双曲线的渐近线的距离会越来越小(如上页图所示).
到双曲线的渐近线的距离会越来越小(如上页图所示).
[3] 这两条直线的方程可以统一记为 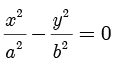 ,这和双曲线的标准方程
,这和双曲线的标准方程 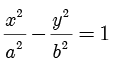 很像,方便记忆.
很像,方便记忆.
● 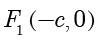 和
和 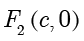 分别称为双曲线的左焦点和右焦点.
分别称为双曲线的左焦点和右焦点.
● 双曲线与 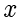 轴的交点为
轴的交点为 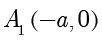 与
与 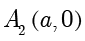 ,与
,与 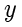 轴没有交点,但是可以标出点
轴没有交点,但是可以标出点 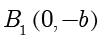 和
和 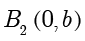 .
.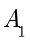 和
和 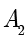 分别称为双曲线的左顶点和右顶点.
分别称为双曲线的左顶点和右顶点.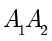 称为双曲线的实轴,
称为双曲线的实轴,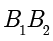 称为双曲线的虚轴.
称为双曲线的虚轴.
● 对于双曲线上的点 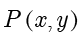 ,有
,有 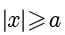 .
.
例题1.4(取自2012年四川卷理数) 动点 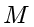 到两定点
到两定点 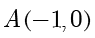 、
、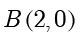 构成
构成 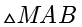 ,且
,且 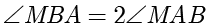 ,设动点
,设动点 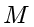 的轨迹为
的轨迹为  ,求轨迹
,求轨迹  的方程.
的方程.
解答 设 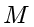 的坐标为
的坐标为 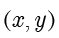 ,其中
,其中 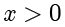 ,
,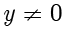 .当
.当 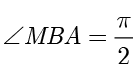 时,点
时,点 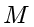 的坐标为
的坐标为 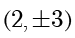 .当
.当 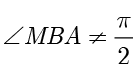 时,
时,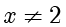 ,由
,由 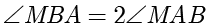 可得
可得
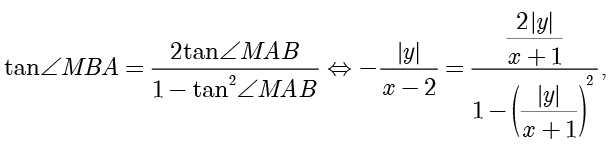
化简可得 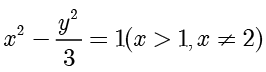 ,而点
,而点 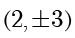 在曲线
在曲线 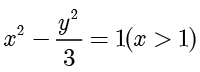 上,因此轨迹
上,因此轨迹  的方程为双曲线
的方程为双曲线 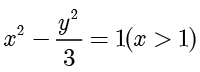 . ■
. ■
在椭圆和双曲线中常常出现根据已知条件求离心率 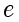 的题目. 一般来说,这类题目需要使用椭圆或双曲线的定义(到焦点的距离之和或距离之差为定值),结合已知条件得到
的题目. 一般来说,这类题目需要使用椭圆或双曲线的定义(到焦点的距离之和或距离之差为定值),结合已知条件得到 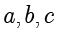 所满足的方程,在此基础上求解离心率
所满足的方程,在此基础上求解离心率 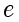 .
.
例题1.5(取自2024年新课标Ⅰ卷) 设双曲线 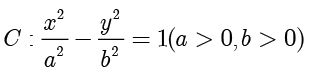 的左、右焦点分别为
的左、右焦点分别为 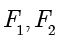 ,过
,过 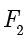 作平行于
作平行于 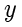 轴的直线交
轴的直线交  于
于 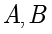 两点,若
两点,若 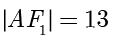 ,
, 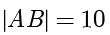 ,则
,则  的离心率为 .
的离心率为 .
解答 将 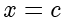 代入
代入 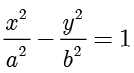 ,解得
,解得 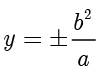 ,因此
,因此
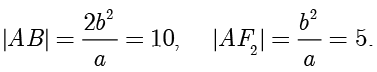
根据双曲线的定义,有 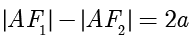 ,整理得
,整理得 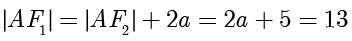 ,据此解得
,据此解得 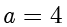 ,
,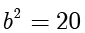 .因此
.因此 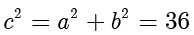 ,解得
,解得 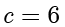 ,所以
,所以  的离心率
的离心率 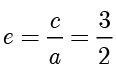 . ■
. ■
在求椭圆或者双曲线的离心率时,有时候需要灵活地使用勾股定理或者余弦定理.
例题1.6(取自2023年新课标Ⅰ卷) 已知双曲线 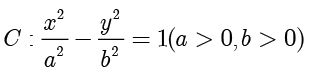 的左、右焦点分别为
的左、右焦点分别为 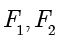 ,点
,点 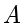 在
在  上,点
上,点 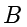 在
在 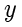 轴上,
轴上, 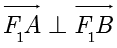 ,
,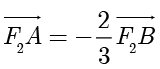 ,则
,则  的离心率为 .
的离心率为 .
解答 设 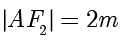 ,则
,则 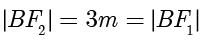 ,
,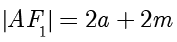 .在直角
.在直角 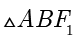 中,由勾股定理得
中,由勾股定理得
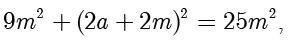
解得 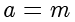 或
或 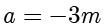 .并且根据
.并且根据 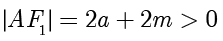 ,舍去
,舍去 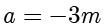 .所以
.所以 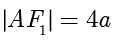 ,
, 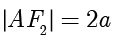 ,
,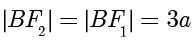 ,则
,则 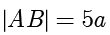 ,故
,故 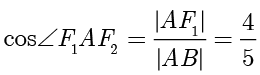 .最后,在
.最后,在 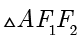 中,由余弦定理得
中,由余弦定理得
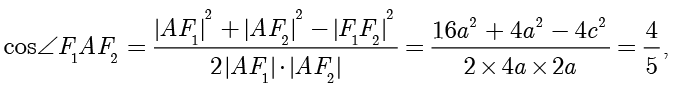
整理得 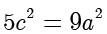 ,所以
,所以  的离心率
的离心率 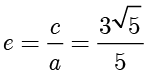 . ■
. ■
例题1.7(取自2024年九省联考) 设双曲线 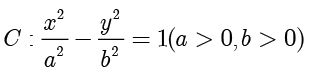 的左、右焦点分别为
的左、右焦点分别为 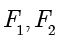 ,过坐标原点的直线与
,过坐标原点的直线与  交于
交于 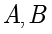 两点,
两点,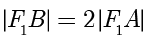 ,
, 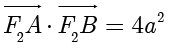 ,则
,则  的离心率为 .
的离心率为 .
解答 根据题意得四边形 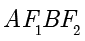 为平行四边形,设
为平行四边形,设 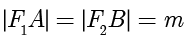 ,则
,则 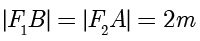 ,由双曲线定义可知
,由双曲线定义可知 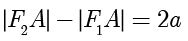 ,故
,故 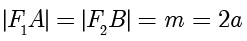 ,
, 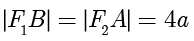 .计算得
.计算得
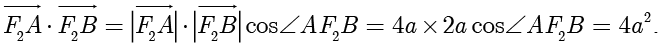
解得 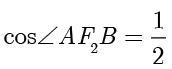 ,因此
,因此 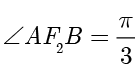 ,
,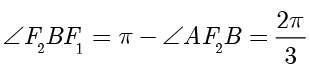 .在
.在 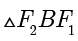 中,由余弦定理得
中,由余弦定理得
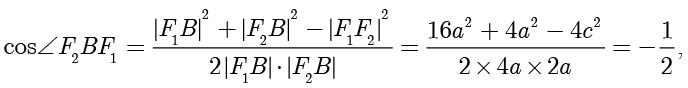
整理得 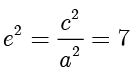 ,解得
,解得 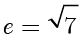 . ■
. ■
例题1.8(取自2025年全国二卷) (多选题)双曲线 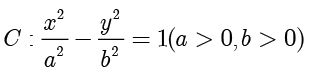 的左、右焦点分别是
的左、右焦点分别是 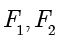 ,左、右顶点分别是
,左、右顶点分别是  ,以
,以 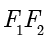 为直径的圆与
为直径的圆与  的一条渐进线交于
的一条渐进线交于 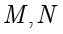 两点,且
两点,且 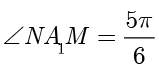 ,则( ).
,则( ).
A.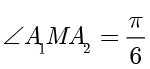
B.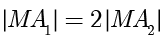
C. 的离心率为
的离心率为 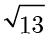
D.当 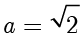 时,四边形
时,四边形  的面积为
的面积为 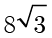
解答 如下图所示,设以 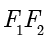 为直径的圆与
为直径的圆与  的渐进线
的渐进线 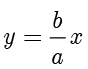 交于
交于 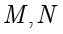 .联立
.联立
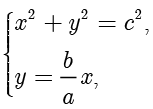
解得 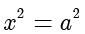 ,故
,故 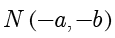 ,
,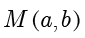 ,所以
,所以 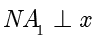 轴,
轴,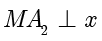 轴,进而
轴,进而 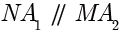 .
.
例题1.8 示意图
对于 A 选项,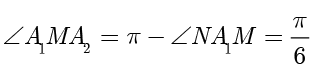 , A 选项正确.
, A 选项正确.
对于 B 选项,由几何关系得 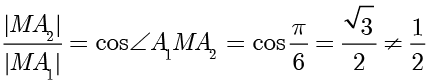 ,B选项错误.
,B选项错误.
对于 C 选项,计算得 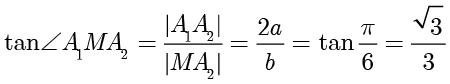 ,整理得
,整理得 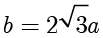 ,因此
,因此 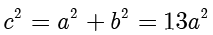 ,
,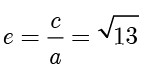 ,C 选项正确.
,C 选项正确.
对于 D 选项,当 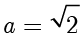 时,
时,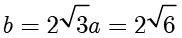 ,因此四边形
,因此四边形 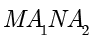 的面积
的面积
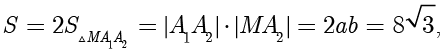
D 选项正确.故选 ACD. ■
和椭圆、双曲线不同,抛物线的定义不再是到两个点的距离之和或者距离之差为定值的动点的轨迹.抛物线的定义如下.
定义1.3(抛物线) 设 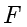 是平面内的一个定点,
是平面内的一个定点,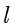 是不过点
是不过点 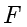 的一条定直线,平面上到
的一条定直线,平面上到 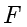 的距离与到
的距离与到  的距离相等的动点的轨迹称为抛物线.其中,定点
的距离相等的动点的轨迹称为抛物线.其中,定点 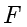 称为抛物线的焦点,定直线
称为抛物线的焦点,定直线 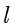 称为拋物线的准线.
称为拋物线的准线.
设抛物线的焦点 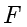 到准线
到准线 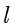 的距离(称为焦准距)为
的距离(称为焦准距)为 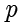 .在平面直角坐标系
.在平面直角坐标系 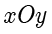 中,设焦点
中,设焦点 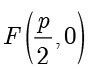 ,准线
,准线 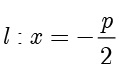 ,并设
,并设 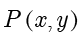 在抛物线上,满足到
在抛物线上,满足到 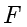 的距离与到
的距离与到 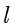 的距离相等,如下图所示.下面推导抛物线的方程.
的距离相等,如下图所示.下面推导抛物线的方程.
平面直角坐标系xOy中的抛物线
根据定义,可得
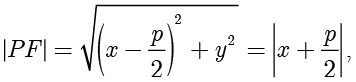
等式两边同时平方并整理,可得抛物线的标准方程
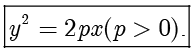
对于抛物线,规定其离心率 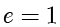 .
.
例题1.9(取自2022年乙卷理数) 设 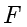 为抛物线
为抛物线 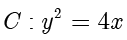 的焦点,点
的焦点,点 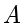 在
在  上,点
上,点 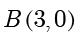 ,若
,若 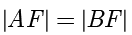 ,则
,则 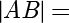 .
.
解答 由题意得 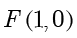 ,则
,则 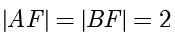 ,即点
,即点 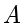 到准线
到准线 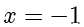 的距离为 2 ,所以点
的距离为 2 ,所以点 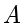 的横坐标为
的横坐标为 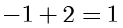 ,代入抛物线方程得点
,代入抛物线方程得点 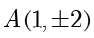 ,所以
,所以
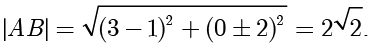 ■
■
例题1.10(取自2025年全国二卷) 设抛物线 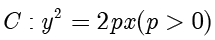 的焦点为
的焦点为 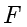 ,点
,点 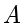 在
在  上,过点
上,过点 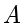 作
作  的准线的垂线,垂足为
的准线的垂线,垂足为 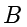 ,若直线
,若直线 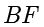 的方程是
的方程是 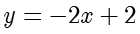 ,则
,则 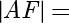 .
.
解答 在直线 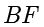 的方程中,令
的方程中,令 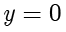 ,可得
,可得 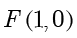 ,因此
,因此 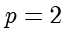 ,抛物线
,抛物线  的方程为
的方程为 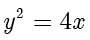 ,准线方程为
,准线方程为 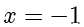 .在直线
.在直线 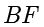 的方程中,令
的方程中,令 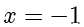 ,可得
,可得 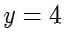 ,故
,故 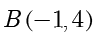 ,解得
,解得 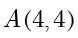 .最后由抛物线的定义可知
.最后由抛物线的定义可知 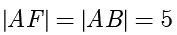 . ■
. ■
在课本中,除了前面所讲的圆锥曲线的方程,还介绍了焦点在 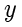 轴上的椭圆、双曲线和抛物线的方程.为了得到这种情况下的圆雉曲线的方程,只需要交换变量
轴上的椭圆、双曲线和抛物线的方程.为了得到这种情况下的圆雉曲线的方程,只需要交换变量 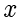 和变量
和变量 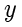 .本书主要以焦点在
.本书主要以焦点在 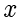 轴上的圆锥曲线为例,因此在这里不多加介绍焦点在
轴上的圆锥曲线为例,因此在这里不多加介绍焦点在 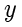 轴上的圆锥曲线.
轴上的圆锥曲线.
本小节探讨下面的问题:设  是平面内的两个定点,动点
是平面内的两个定点,动点 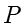 到这两个点的距离之比为定值
到这两个点的距离之比为定值 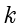 ,即
,即 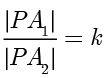 ,那么点
,那么点 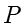 的轨迹是什么?如果
的轨迹是什么?如果 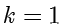 ,那么
,那么 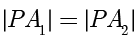 ,此时点
,此时点 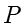 的轨迹是线段
的轨迹是线段 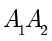 的垂直平分线.下面研究的是
的垂直平分线.下面研究的是 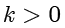 且
且 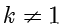 的情况.
的情况.
在平面直角坐标系 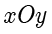 中,设
中,设 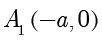 ,
,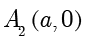 ,
,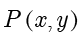 ,则有
,则有
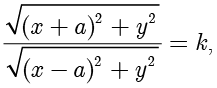
等式两边同时平方并移项整理得
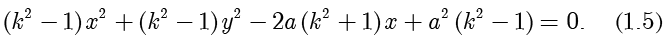
读者应该记得,当且仅当 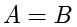 ,并且
,并且 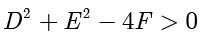 时二次方程
时二次方程 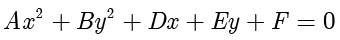 表示圆.在上面的方程中,
表示圆.在上面的方程中,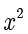 项和
项和 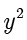 项的系数相等,并且计算得
项的系数相等,并且计算得
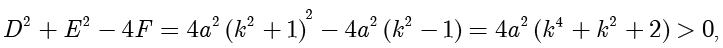
因此方程(1.5)表示圆.这个圆称为阿波罗尼奥斯(Apollonius)圆.特别地,当 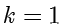 时,可以将线段
时,可以将线段 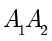 的垂直平分线理解为“半径为无穷大的圆”.
的垂直平分线理解为“半径为无穷大的圆”.
例题1.11 (取自 2008 年江苏卷) 满足 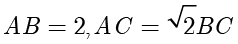 的
的 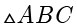 的面积的最大值是 .
的面积的最大值是 .
解答 以 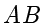 所在直线为
所在直线为 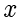 轴、
轴、 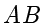 中点为坐标原点
中点为坐标原点 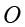 ,建立平面直角坐标系
,建立平面直角坐标系 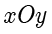 ,则
,则 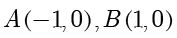 .设
.设 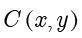 ,由
,由 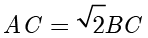 可得
可得
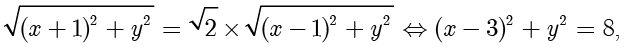
即点  在以
在以 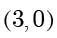 为圆心、
为圆心、 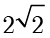 为半径的圆上,因此点
为半径的圆上,因此点  到直线
到直线 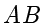 的距离的最大值是
的距离的最大值是 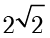 ,从而
,从而 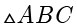 的面积的最大值是
的面积的最大值是 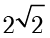 . ■
. ■
在学习圆锥曲线的定义之后,读者可能会有这样的疑问:为什么圆锥曲线中会有“圆锥”二字?事实上,圆锥曲线最早是通过平面截圆锥发现的,如下图所示.设平面不经过圆锥的顶点.从图像可以看出,当平面不与圆锥的母线平行且只与圆锥的一侧相交时,交线为椭圆;当平面不与圆锥的母线平行且与圆锥的两侧都相交时,交线为双曲线;当平面与圆雉的母线平行时,平面只能与圆锥的一侧相交,交线为抛物线.
平面截圆锥得到的椭圆、双曲线和抛物线
以椭圆为例,设平面不经过圆锥的顶点,不与圆雉的母线平行且只与圆锥的一侧相交,下面证明平面截圆锥所得到的曲线符合椭圆的定义.设点 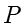 在截面上,为了证明点
在截面上,为了证明点 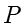 到两个焦点的距离之和为定值,需要先找出两个焦点
到两个焦点的距离之和为定值,需要先找出两个焦点 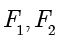 ,所以在这里构造两个球进行辅助,这两个球称为丹德林(Dandelin)双球,如下图所示.
,所以在这里构造两个球进行辅助,这两个球称为丹德林(Dandelin)双球,如下图所示.
丹德林双球示意图
在截面上方作圆锥的内切球 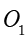 ,同时与截面切于点
,同时与截面切于点 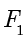 ;在截面下方作圆锥的内切球
;在截面下方作圆锥的内切球 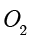 ,同时与截面切于点
,同时与截面切于点 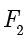 .设
.设 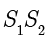 是球
是球 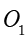 和球
和球 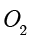 在圆锥的母线上的公切线.过点
在圆锥的母线上的公切线.过点 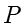 沿着圆锥的母线作球
沿着圆锥的母线作球 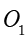 和球
和球 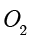 的切线
的切线 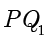 和
和 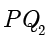 ,与两个球分别切于
,与两个球分别切于 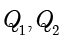 两点.根据球的切线长性质,得到
两点.根据球的切线长性质,得到 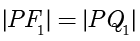 ,以及
,以及 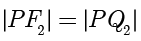 ,因此
,因此
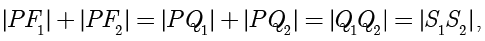
其中 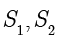 是定点,因此
是定点,因此 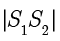 是定值.这便证明了点
是定值.这便证明了点 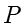 在以
在以 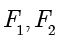 为焦点,以
为焦点,以 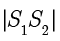 为长轴长的椭圆上.
为长轴长的椭圆上.
例题1.12(多选题) 如下页图所示,小黄家的墙上固定了一盏圆锥(截面 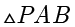 为等腰直角三角形)状的灯,灯光可以照亮的部分是一个无限大的圆台,其截面的边界分别垂直于
为等腰直角三角形)状的灯,灯光可以照亮的部分是一个无限大的圆台,其截面的边界分别垂直于 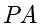 和
和 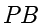 .已知墙与地板垂直,灯向上或向下转动的极限均为
.已知墙与地板垂直,灯向上或向下转动的极限均为  (即
(即 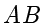 可以绕
可以绕 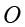 点顺时针或逆时针旋转
点顺时针或逆时针旋转  ).若地板和墙都充分大,则灯光照在地板上的边界的可能形状有( ).
).若地板和墙都充分大,则灯光照在地板上的边界的可能形状有( ).
A.椭圆
B.双曲线的一支
C.抛物线
D.一条直线
例题1.12示意图
解答 根据题意,灯光可以照亮的部分是一个无限大的圆台,该问题可以转化为用平面截圆台所得截面的问题.固定灯 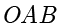 不动,考虑将地板从
不动,考虑将地板从 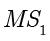 旋转到
旋转到 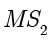 ,设
,设 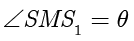 ,如下图所示.根据圆锥曲线的定义可得:
,如下图所示.根据圆锥曲线的定义可得:
固定灯 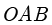 不动,将地板从
不动,将地板从 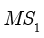 旋转到
旋转到 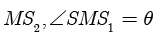
● 截面与圆台的轴平行时,截得双曲线的一支;
● 截面与圆台的母线平行时,截得抛物线;
● 截面不可能只与圆台的侧面相交,因此不能截得椭圆;
● 截面不可能与圆台的侧面相切,因此不能截得直线.
故选 BC . ■